1. Theorems / 定理
2. Lemmata / 補題
3. Definitions / 定義
4. Axioms / 公理
5. Conjectures / 予想

　1. Theorems

　鏡にはぼくがいる。
　そのぼくの背後の鏡にまたぼくがいる。そのぼくの背後の鏡にまたまたぼくがいる。鏡、鏡、鏡、また、また、また。限りなく顔は連なる。１，２，３……自然数全体の集合の大きさ、すなわち＜可算濃度＞《アレフ・ヌル》と表される無限だけある。
　ぼくは首を横に振る。
　鏡内ぼくは首を縦に振る。鏡内鏡内ぼくは肩を揺らす。鏡内鏡内鏡内ぼくはジャンプする。鏡内鏡内鏡内鏡内ぼくは笑って胸の真ん中を指す。
　肌から盛り上がった白い繭。
　鏡のぼくらはみな繭に触れ、そのはしをつまむと爪を入れ、ほつれた糸をつまんで引いていく。繭は縦軸を中心に回転し、きりきりと音を立てながら、ぼくらめいめいの指先へ届く色のグラデーションを糸に与える。そして腕の長さだけめいいっぱい張られたら多色の糸は震えだし、指から離れて、四方八方へと伸びていく。鏡に切り取られた外側、無色の空に流れ、己が振動の音を背景に踊り出す。
　ぼくの足がうずうずしているのを察したように、鏡のぼくが、さあ、と言う。
　ぼくはうなずき、胸の真ん中に指を入れる。
　なにもない。
　ぼくは叫ぶ。風に殴られたように糸が巻き上がり、鏡面を滅多打ちにする。鏡が割れ、亀裂を境にわかれたぼくらの顔や手は、落下する無数のピースとなる。糸の残像だけが鏡面から浮き上がり、ぼくの胸に突進する。中心の空洞が糸の先端を喰らい、与えられる弦を呑み、闇のなかどこまでも風切る音だけがする。

　目覚めると体が重く、ぼくの胸の中心には、いつも通りに＜証明繭＞が填まっていた。
　この夢のことを、ある友達と山を歩いている最中も忘れられずに話し出すと、
「待ってくれ。『そのぼくの背後の鏡にまたぼくがいる』だって？　合わせ鏡なら、鏡の鏡の自分は鏡の自分の後ろに隠れちまってるんじゃないか？」
「鏡と鏡が真向かいになってなくて、少し角度があったんだよ」
「なら自分の数には上限がある」
　かれは土に木の棒で、向きの少しずれた鏡二枚の間で反射を繰り返す光の経路図を描く。一方の鏡を発した光線は、他方の鏡に届くと反射し、角度をつけて元の鏡でまた反射し、三角形の階段をつくるように上がっていく。すると光は有限のステップで鏡を飛び出してしまう。
「鏡の長さに限りがなかったか、鏡の曲がり方が特殊だったんだと思う」
　ようやく納得した様子のかれだったが、話が進むと、「見えてない空の色がどうして無色だとわかるんだ？」と言い出した。こういう議論はぼくらの村じゃふつうのことだ。特に、かれからぼくへの話のなかでは。ただこの前、トポロジー系のものたちの住む真実伸縮森林街に旅行して、ぐにゃんぐにゅんぐにょんな暮らしのゆるさに当てられたことが、ぼくの口をむずむずさせた。
「神経質だね」
「おまえがずさんなんだろ」
　当然そうだ、というような物言いだった。
「そうだね」
「そうだ」
　それで終わり。なんとなく気が抜けたけれど、ここで話を止めるのも、かれの完璧主義傾向からして気に障りそうだから続けた。胸の中心に感触がなかった段で、
「繭をなくした夢だって？」
　ドリルのような鋭利な声。ぼくは取り繕うようにほほえもうとする。「夢だよ」
「気色悪い。正夢じゃないのか？」
「大丈夫だよ」
　ぼくは胸の真ん中から小指の頭分だけ飛び出ている証明繭を撫でる。
　柔らかな手触りの繭は、かすかにさざ波のように脈打っていて、ほんのりと暖かい。この星中の繭とエネルギーをやりとりしている証だ。同時に、＜定理＞たるぼくの存在証明でもある。
　ぼくらは額に定理の主張（ステートメント）を、胸に定理の証明を宿す。証明とは、前提から出発して、結論に辿り着く、論理でできた道のようなものだ。――ぼくらの場合、記号的な論理体系の地盤上で、大前提に当たる＜公理＞から出発して、結論の＜定理＞に至るもの。これがないと、定理は定理、つまり正しいと確認される命題ではなくなってしまう。すなわちぼくらはでたらめなのっぺらぼうとなってしまう。この大地とのつながりも失われてしまう。
　ぼくが見たのは夢だった。恐ろしいだけの夢ではなかった。無数の糸が舞い踊り虹のように色とりどりに輝く世界があった。けれど――冷静になって、他人の目にさらせば、変な話、だ。
　今きちんと繭はある。それを確認したくてぼくは繭をこすった。友達はばかげたものを見てしまったというような目をした。
「まあ気をつけろよ。＜漂流定理＞みたいに、繭がだめになっちまったやつがいるっていうんだ。根拠のある忠告だからな」
「まさか。圧制者のせいで情報蒸発させられた我らが中世暗黒時代のことじゃないでしょ？」
「つい最近だよ。おまえが留守にしてたときに、おれたちみんなで聞いた。なんでも……、おれの親によると、自分で切ったんじゃないか、って話だよ」
「嘘」
「ま、ろくでもない証明だったのかもな。持っているほうが嫌になるような、さ。おれには考えつかないが――おまえなら、わかるんじゃないか？」
　ぼくは手を離そうとしたが、手は逆に繭を隠した。かれは見逃さず、じっと目を合わせてくる。「理解者だよ」と気取るような余裕ぶりかただった。
「何のこと」言ってしまったとたん、かれの表情が破れる。
「ほら、おまえ、わりとさ。いびつだろ。主張（ステートメント）も、繭も」
　あからさまにかれがそう言うのは初めてだった。ついにか、と、額をこすり、ぼくは思った。やっぱりか、今日だったか。衝撃を受けたとき、感情がわからなくなって、思考だけが動いていることが少なくない。今もそんな感じで、どういう表情をすべきか迷いながら、この事態を認識していた。
　認識していた：額に刻まれた主張（ステートメント）を指の肉が埋めていた。具体的な数値評価を盛り込んで、楔数とハーディ＝ラマヌジャン数との関係を記している主張は、かれの額の刻む、抽象的概念ばりばりのものに比べると、いかにも下町くさいんじゃないか。
　同時にかれの胸の中心の繭を見ていた。ヒトならサファイアのようにと言うかもしれない青の輝きはほとんど上下左右対称の菱形で、つんと盛り上がった奥に、アクロバティックな証明を秘める予感がある。ぼくの繭は薄茶色、濃淡はむらがあり、形状の左右バランスも満月から下弦の月に１／３程度進んだ形のようにずれている。かれはこの繭のことを指摘している。妥当――正当――しかたなし――でも狩人の底知れぬ残酷さをたたえる眼差しの射程はここに留まらないとぼくの背がうずいている。繭を紡ぐ＜証明糸＞、そして証明の構成まで、批判の射程に入れている、だろう――。

　ぼくらについての「証明」は、特に、形式化された数学の論理の上での証明を指す。記号的な論理体系の上で、大前提に当たる＜公理＞から出発して、結論の＜定理＞に至るという道筋だ。
　記号的な論理体系は、推論の上で使える記号（∧：かつ、∨：または、￢：否定、⇒：ならば、など）の集まりと、たとえば「『ｘ⇒ｙ』から『ｙ∨￢ｘ』を導くことを許す」といった、論理展開の規則の集まりとも翻訳できる。
　そんな道筋や規則はこの星だと空間描像で表現される。第一に、胸の証明繭や、ぼくらの暮らす陸地の姿だ。陸地は大まかに、論理体系にあたる数個の＜形式大陸＞でなり、大陸上には公理に相当する＜公理大樹＞が立っている。一方、ぼくらの証明繭は、隠れた次元方向に伸びる空間バンドル上で星を取り巻く＜情報膜＞を介して、この公理大樹とつながっている。大陸や大樹の情報は膜上に模様として刻まれ、大樹の模様をくるむ閉じたひも――＜公理ひも＞へ、証明繭をなす証明糸の別の姿に相当する、開いたひも＜証明弦＞が一端をつけているのだ。この、膜関連が第二の空間描像。こちらをぼくが観たのは、教材としてスクリーンに投影された録画映像でだけだった。以前自分のを観たらどうかと思ったけど、親が幾何学や関数論から受け取った雑多な証明手法を、つぎはぎし、泥臭い計算の弦でつないでいることが想像されて嫌になった。
　そう思い出した最中だったから、ここに来たかれの次の言葉は、過冷却した冷水を一挙に凍らせるような一撃だ。

「実はさ」何気ないふうにかれは加える。「逆にな。とっくにおまえの証明弦が切れかけてて、そのせいで繭もひしゃげてるんじゃないかって心配してたんだよ」
「ばかな、そんな」
「確認したことあるか？　自分の弦」
　ないけど。口ごもる。
「おれはある」ゆっくり、じっくり、かれは言う。「おれが生まれたときのを記録したんだ。すごいんだぜ、弦を親から受け継いだのがよくわかって――あ、おまえも観たよな。ま、いいや。だからおぼつかないはみだし定理――かすらわからないやつから目を離せなくてさ。一応同じ土地に住んでる近代定理同士だし、世話も義務だろ」
　目を離さなかったのはぼくのほうだ。かれは、自分から言い出してぼくと遊びに行くときでも、いざ出発すれば、仕方ないつき合ってやろうという立場に翻り以後ポーズを崩さなかった。そういう傲岸をぼくは放置、いや、あきらめの上で肯定していた。かれは美しく、ぼくはひねくれていたから。今も美しい。腰を巻く布に両手をつき、狩人顔から得意顔から憐れみ顔に変じたかれの造形には、建築構造の整然たる感がある。なんといっても胸の中心の繭。教育映像で再生された誕生時の光景には、水晶のように透き通る圏論的な遺伝子を親たちから受け継いだかれの弦があった。
　素数波が海に交響曲を奏でているときにかれは生まれた。ぼくら数にまつわる＜数論＞関係定理たちの、まだ新しい顔の中でも、将来を期待されている。それゆえに自負せざるを得なくなったんじゃないかとぼくはこそこそ解釈し、ああだこうだ言われても、けちをつけられ貶されても、使いっ走りを頼まれても、アトラクタ・アトラクションで定常軌道を巡らされる実験台にされても、羽目を外して同じ場所に落下したかれを救出させられ反動でぼくは海に落下しても、結局誇らしい気分にもなってしまう。友達だという位置づけがうわべだけの慰めだと気づいていても。いてもその上で、関係から抜け出さないことを肯定していると思っていた。
「えと……君は、その、ぼくのことを……ずっとそう思っていたの」
　しかしぼくの舌はつっかえる。ぼくの手は完全に繭を覆っていた。ここに感触があってもかれの意地悪な批判をはねのける何の助けにもならないのに。
「おれだけじゃない」かれは苛立たしげに一歩引いた。「みんなだ」
　いつものように「そうだね」と受け入れずにみっともなく食い下がる姿が耐えかねたのだろう。でなければ窮屈になった空間に我慢できなかったか。なにか探すように手を叩くと、「そもそも親が怪しいじゃないか。別の地域から流れ着いてきてさ、村の隅っこの日陰で暮らしてて。建築のためとか言うけど、本当は居場所がないから来たんだろ？」
「親は――」
　最近は顔を真正面から見ていない親たち。自分で「雑多な証明手法」と思っておきながら、喉が熱くなった。「親は、違うだろ」
　かれの名を友達として出すと親たちは安心の様子を見せた。親たちは望みでもしているふうだった――自分たちの家系にかれの受け継ぐエレガントな証明弦の遺伝子が入らないかと。実現のありえない希望、あるいはお笑いの風景だ。ぼくは親を騙しているような気がしながらかれの名を出し、欺くのが重荷になって、顔を見ないようになってきていた。
「へえ」かれは眉を上げる。「ま、とにかくさ。心なき＜漂流定理＞とも違う、おれたち人格の育った定理が繭をなくすと、本当にまずいんだからな。証明繭がいかれたら、繭の弦に巻かれて形を保っている＜人格管＞も、破裂しちまうか萎んじゃうだろう。例のそいつも無反応のほぼ屍だってよ。となればおれたちの大切な思い出だって、塵か泥だ。気をつけてブラシでもかけるといいさ」
　ようやく感情の本流が帰ってきた。
　憎みたい。
　ついにわかった。事実こいつを憎みたい。ああ、ぼくの目に映るかれが、かれの目に映るぼくのように醜い定理であれば。であれば憎めたろう。しかしかれの主張（ステートメント）はそして証明繭は非の打ち所なく格好良かった。ハンサム、クール、美形、玲瓏、カンカンのキラキラだった。ぼくは屈折して恥じ入った。みっともなく震えだした両手を背中の裏へと隠した。
　憎むべきはぼくとなった。蔑まれ憐れまれ気遣われる醜さが問題なのだと膝を折り、ぼくはヒキガエルの笑顔を作った。
　かれは光を背に、腕を開き、従者を許す寛容さを見せた。一方の手を差し出してくる。ぼくは膝を折ったままで顔を伏せ、こわばる肘を持ち上げる。形式的和解、実質的臣従の儀式たる握手の場へと、指を伸ばす。かれの手からの熱輻射を感じ取れるほどになって目を閉じ、手のひらを叩きつけた。
　衝突音のかわりに、木の割れる音が聴覚を占めた。
　目を開けば真っ二つで横倒しの枯れ木の上に、岩塊。その手前で、「――あなたは」元友達は、体を捻って尻餅をついていた。
　逆光の岩から空へ伸びるすらりとした立ち姿。胸の豊かな繭は陰にて虹に輝き、額の主張も自ずから明るさをにじませているかのようだった。

　Profile 1.1
　――「複素多様体上の正則関数の層は連接である」
　その主張を刻むのは伝説的な定理、＜岡の連接定理＞だ。＜古代定理＞、すなわち、星のシステム的本体である演算系が走り出すよりも昔、ヒトが発見した定理の一員だった。しばらく前に隠棲したと聞いていた。

　なぜここにいるのか？　行動学的疑問は、降って湧いた光の前ではどうでもいい。だが元々友達にして元ボスは粗雑に尋ねて沈黙の香りをふいにした。
　古代定理は微笑した。
「きのう見つけた漂流定理を、＜平方剰余の相互法則＞に世話してもらおうと頼みに来たの。今は帰り。浮かんで歩いてたら魔が差して、落ちた。まだまだ修行が足りないみたい」
　古代定理も修行するのか。
「あの、――おれ、夢があって。素晴らしい定理の証明弦の一部を、おれの弦と掛け合わせたい。未来の礎となる素晴らしい定理を生みたいんです」
　ぼくは反射的に目をそらす。
　――美しいと思われ、優れていると思われる存在たちと子をつくること。それはかれが自分に課してきた目標のはずだ。夢というよりも確信、そして通過点として。
　ぼくら定理には性別もなく、ともにひとつの子をつくる相手も１，２，３，４……いたって構わない。しかし無作為ではない。相手は選びあうものだ。かれは期待し、ぼくは放棄している。この一文を世の理のようにぼくは見なしていたが、今、その瞬間を見つめるのはできなかった。
「そう」
　古代定理は優しげに言った。「それで、上空飛行に興味は無い？　いわば進む空間の拡大ね。鳥みたいに飛ぶというより、このままの形で……」
　かつての友達は拳を握って瞬いている。ぼくも唖然としていた。あのアプローチに何一つ関心がないふうな存在を、初めて見た。このとき、ぼくは元友達を、いい気味だとも残念だとも思わなかった。胸が、張り裂けそうに、期待を告げた。
「あの――」
「試してみる？」
「いえ、あの。ぼくの証明繭――ちゃんとしてますか？」
　ただ、一歩近付きたい。
　言ってから恥ずかしくなって目を伏せると、さらりと手が伸びてきた。中心に指先で触れられたとたん、形あるはずの繭がほどけていくような弛緩する感じに包まれる。
「……なつかしい」
　頬に囁きが落ちて引き戻される。「あなたからヒト２０世紀の香りがする。暑い土地と餓えた土地、共鳴。神殿。＜魔術師＞と呼ばれた数学者の見いだした定理を思い出す。――その証明弦も楕円曲線とＫ３曲面を経由しているのね。懐古的でごめんなさい、あなたのことを＜１７２９＞と呼んでもいい？　３番目のカーマイケル数、２６１番目の楔数、そしてはじめのハーディ＝ラマヌジャン数」
「ぼくを」
「ええ。わたしのことは＜連＞と呼んで。いつか空を行きましょう」
「……それは、ちょっと、考えさせてください」
　なにかよく分からなくなりしゃべりだけすると、かれは声を上げて笑う。その瞬間、虹に輝く豊かな繭が、二重になったような気がした。
　けれどそんなことありえない――ぼくは妄想を打ち消す。星ができる前も、できてからも、何十何百何千の定理に引用されてきたこの定理（ひと）に、そんな変なことがあるなんて。
　一方で、ぼくは横に立つものを見た。日々絶やさぬでいた調整を切らした表情を見ると憎さも失せた。かれと子ができたなら実際どんなふうだろうとかすかに思ってみたのが、遠く遠い昔のことだった。
「そうだった、＜１７２９＞、あなたの繭に問題はない。じゃあ、また」
　連接定理はふわりと下の林に飛び降りた。元友達はしばし呆然と立ち、ぼくを殴るふりをしかけてから拳をおろすと、あらぬかたへと駆けていった。ぼくは家を出、元友達を二度見ないうちに千日が経った。

　トゲだらけの赤い葉が降ってくる雑木林を駆け抜ける。葉は表裏反転した二つの像を重ね合わせて舞い降り、土に吸い込まれていく。
　前来たときは、空を覆う深緑の樹冠と薄ベージュの木肌、どこから発するのか分からない熱気に満ちていた林は、今ではわずかな肌寒さを覚えさせる。ここには「四季」がある――そんな地域をぼくはこの島のほか知らない。
　連の住むこの島は、ぼくの暮らす地でもある＜古典論理大陸＞（大陸の中でも大きい場所だとぼくは思っていた。大きさをきちんとはかる基準がなにかが問題だけど）の端っこに浮かんでいる。一応＜情報膜＞上では、大陸中央の公理大樹とつながっているらしい。でも、連以外の定理（ひと）を見たことはない。
　なぜこんなところに住んでいるか、連に聞いたことがある。
「形式から離れられる気がするから」
　初対面ではその主張の綺麗さに目と思考力を奪われていたが、連はなかなか不思議なところがある。古代定理だからかもしれない。古代中の古代、＜三平方の定理＞なんて、ひ孫玄孫の幾何定理連中がキャッチボールに使っている曲がりくねった曲面（その上では平行線が何カ所でも交わったり決して交わらなかったりする）を煙たがって、直線だらけの山奥に隠棲しているし。

　ともあれ今日は報告がある。
　ぼくは林の最後の幹を越せば開ける視界の真ん中、なだらかな丘の上にある山吹色の屋根まで一息に駆け上がり、直下のドアに飛び込んだ。
「さっき定理が生まれたよ、＜指数定理＞！」
　横顔の連がこちらを向く。好奇心以上に惹かれているときの目の色だ。やった。この定理の名前は、「いつか生まれる」と連がお待ちかねのリストにあったのだ――だから急いで報告に来た。ぼくが新定理の親たちの名を言えば、
「そう、アティヤ＝シンガーの系譜を辿ったのね」
　赤らんだ頬で試作中のリーマン面クラフトを撫でる。「闇の時代を耐えられず消えてしまったあの定理（ひと）が、やっと生まれ変わったのね。……。もとの古代定理が系譜を追って生まれていく。わたしたちの歴史も、ようやくヒトのものに似てきたのかしら」
「似てても似てなくてもいいじゃないか」
　ヒト数学者の時代をあまりに特別なように言われると、正直少し反発を覚える。古代定理しか実体験のない時代。ぼくには真の意味で共有できない歴史。
　定理誕生を報告して喜んでもらいたかったのに、ひとりの世界に行かれた気分だ。
　――第一、ヒトなんて、それこそ＜演算革命＞で、圧制者ごと乗り越えられた存在じゃないのか。
「そうね、昔の定理でも、今の定理でも、ここに生まれたことは祝うべき。行きましょうか、誕生祝い」
「そのお祝いはどうかと思う」
　円卓から、ひもでできた長四角の枠をとりあげた連の前で、ぼくは首を横に振る。
　「カントール集合的ほとんど透明ショール」という代物だ。ひもでできた枠の内側はほとんど透明。面積体積も外枠の分しかない。でも手をつっこむと繊維の感触がある。同じような布地は「着ていないふうに見せて着ている」というファッションにも使われるけれど、赤ん坊には刺激が強すぎると思う。

　ショールは一種のフラクタル洋服：同じパターンが入れ子になっている服で、詳しい製法は次の通りだ。

　Recipe 1.2
　(1) まず、ひもの内側に長方形の布を張り、左端より 1/3 から 2/3 地点までの部分をすべて切り取る。
　(2) 次に、残った、0 から 1/3 地点（[0, 1/3] と表す）と 2/3 から 1 地点（[2/3, 1] と表す）という 2 区間で、またそれぞれの真ん中 1/3 を切り取る。すると [0, 1/9], [2/9, 3/9], [6/9, 7/9], [8/9, 1] の 4 区間が残る。
　(3) 次のステップでは [0, 1/27], [2/27, 3/27], [4/27, 5/27], [8/27, 9/27], [18/27, 19/27], [20/27, 21/27], [24/27, 25/27], [26/27, 1] の 8 区間が残る。
　(4) 以後同様に繰り返す。“帰納法的”手法。

　Discussion 1.3
　こうしていくと、区間の数はどんどん増えていき、布も決して「消え」はしない。実際、布にある点は、三進法で表したとき小数部分が全部「0」か「2」になっている点である(A)。その総数は、整数全部より多く、最初の布と「同じ分だけある」ことが説明できる。
　一方、面積は、1 → 2 × 1/3 = 2/3 → 4 × 1/9 = 4/9 → 8 × 1/27 = 8/27……と 0 に近付いていく。限りなく操作を繰り返した「布」（極限）については 0 となってしまうのだ。

　Notation 1.4
　ここには、一見、布を表す「無限の点」が表現されているとみえる。でも、空間表現の背後にもともと無数の情報素子（ビット）が準備されている訳ではない。Recipe 1.2 や Discussion 1.3 (A) のような、有限の文字数（よって有限の情報素子）で済む「関数的」記述を、この星の空間表現が許容しているのだ。表現の制御は星の根幹――というか星として空間表現される「正体」：＜演算系＞の担うところだ。^[1]

　有限の文字数で、無限の点を表現する。
　ぼくらはこうして、有限リソースの演算系の上で、無限を意識することができる。

　――無限。有限生成の形式上で表現され、許容される無限。それで無限は終わるんだろうか。

　そう思うと、鼻の奥がつんときて、胸が痛くなった。痛い。結構、うん、かなり痛い。見下ろすと証明繭が赤く光って揺れていた。連のも光っている。
「漂流定理が来たみたい」
　連はショールを置く。残念だが、出動の時のようだ。
　代数、幾何、解析と、数学の諸分野に友達や血縁関係者を持つ連は、漂流定理の鑑別者として頼られている。
　ぼくは根無し草の旅定理ながら、そんな連をときたま手伝う。

[1] 感触について：布オブジェクトへ、関数的に記述された空間情報をもとに、ぼくの指との接触判定が行われる。フラクタル的オブジェクトとの接触判定をいかに迅速に済ませるか／また処理時間がかかりそうなら曖昧値を返却するかは、いくらか工学的な事項だ。曖昧性の演算については、＜ファジー論理大陸＞の技師たちの助けもある。

　2. Lemmata

　霧あふれる針葉樹の並木道を小走りに行けば、木々は回転しながらクラインの壺をまわるように幹の内外を反転させつつ、そのうち幅次元、奥行き次元、高さ次元、と退化していき、気づけば空は青くフラクタル状に凹んだ浜辺がぼくらを迎える。
　砂のこちらまで寄せては返し、返しては寄せる青波が、ぎこちなく一カ所で滞っている。そこは泡の塊だった。発泡スチロールのように固体じみてこわばった白い泡が、ブドウの房みたいに群がっていた。群がられているのは硬質な丸っこいもの。波が退くとき泡が引っ張られて全貌が見え、眼を閉じた禿頭だとわかる。額には長い主張（ステートメント）があるようだ。
　連がその頭を引き上げる。腹まで陸上に出る。定理なら本来証明繭があるべき胸部中央は紡錘形に抉れ、かわりに青色を残す潮水で満ちている。一瞬の後、潮水は失せ、欠落部は光を拒むように真っ黒になる。
　海から離れたから潮水は存在しえない、と、この星の空間描像を統括する＜演算系＞に演算処理されたのだ。そして漂流定理本来の描画仕様――証明繭の欠落部において光の反射は定義されない――が前面に出る。
　おぞましい。
　こみあげる吐き気に、ぼくは、連がこちらを見ていないことを確認してから鼻をつまむ。

　Recall 2.1 ^[2]
　ぼくらは本来定理同士で結びあい、子供をつくる。子供――というのは、親たちの主張を踏まえて論理的に拡張された定理のことだ。子供の証明には親たちの証明の必要な部分が組み込まれることになる。
　ぼくも出生に立ち会ったことがある。
　まず、親となる定理たちが手を結び、円をつくる。すると親定理の証明繭がほどけ、円の中心に光が現れ、しばらく多色に明滅した後、周囲の自然的構成物を吸い込んで、ヒト形をつくる。
　この「しばらく」の間に、＜情報膜＞まわりでは次のことが起こっている――教材となったスクリーン映写でぼくが観た記憶では。
　始めに、親めいめいの証明弦が、情報膜の上にほどけて、振動し、鳴り始める。互いの音の共鳴が、証明複写開始のシグナルだ。情報膜に浮遊する自由論理弦が、ＤＮＡを転写するときのように親たちの証明弦の必要箇所にくっついて、どんどんつながっていく。必要箇所を複写し終えたら、親たちから拡張されるところにあたる部分を論理弦が紡いでいき、すべてのパーツが埋まる。開始の端を公理系ひもにつける。新たな証明弦の誕生だ。
　――そして、地上でのヒト形形成と並行して、人格部分が発生する。新証明弦の下にある情報膜が盛り上がり、その側面に、人格情報と対応する固有の模様を形成していく。俗に＜人格管＞とか＜人格風船＞とか呼ばれるこの模様つき突起は、生まれたての定理ではまだ小さくて成長に伴い拡張するらしい。
　とはいえ小さくても、人格が芽生えた時点で、情報膜上に刻まれている共有知識は利用可能になる。たとえばぼくが知るヒトの歴史も、今使っているヒト由来のこの言語も、そうだ。両者は星上の全定理に共有される情報であるわけだが、実際知識については真偽が謎だし、言語もヒト時代のと同じものかはよく分からない。でも、公理、定義、定理を結ぶ論理が生きていれば、ぼくはよかった。

　Recall 2.2 ^[2]
　漂流定理は、ぼくら、親を持つ定理とは違う。
　ぼくらが誕生時から備えている証明繭を、かれらは欠いている。もしくは不完全な証明弦の断片だけを有するのだ。ヒトなら心臓や脳がないことに相応するかもしれない。しかしかれらにも「定理」としての主張（ステートメント）は、ある。ときにはぼくらの知る語句をつなぎ、ときには意味不明の語句を交え、主張は刻まれている。
　かれらがどこでどのように生まれるのかは謎だ。いかなる公理大樹にも結ばれずに海を流れ、どこかへ漂着する。
　岸に打ち上げられて終わりではない。長いこと放っておかれると、かれらは溶けて乳白色や青緑色などのスープになってしまう。定理として生まれなおすために治療を必要とするのだ。治療とは、額の主張（ステートメント）を読解し、語句の意味がきちんと定義されるように解釈してやって、その主張を成り立たせるための証明（道筋）を埋めてやること。証明充填のプロセスは新定理誕生のプロセスに似ているけれど、生みたいものを生むのではなく、生まれ直したがっている相手の主張を汲む必要があるから、多くのケースで協調性、器用さ、傾聴のような技巧を必要とする。十、二十名がかりでやることもある。
　この前は、ぼくの故郷に「月月月は葉葉である」なんてのが拾われた。長老たちは、「月」からムーンシャイン予想を、「葉」から葉層構造を読み取れるんじゃないか、いやリーマン面の分岐だ、云々かんぬんと言い出して大きな議論になったらしいが、結局「月＝４」「葉＝８」と解釈され、ただのかけ算（４×４×４＝８×８）でおしまいになった。
　一般に、治療の成功を決めるのは、漂流定理の主張（ステートメント）と治療者の相性が大きい。漂流定理と治療者の主張に共通語句が多かったり、構造が似ていたりすれば、成功しやすい。また漂流定理の胸に不完全な証明弦が発見されることもあって、それが治療者のと似たパターンであれば成功率を大きく上げる。
　要はアレだ。治療者から見て「なんかおれたちに近そう」って漂流定理は迎え入れられやすいんだ。逆に誰から見ても「奇異すぎて困る……」ってのは、大抵いろんな分野の定理グループをたらい回しにされ、結局陸で溶けるか、海にお返しされる。
　で、連は、漂流定理の主張をしらべて相性が良さそうな治療者候補を呈示するのが、とても上手い。

[2]　説明を本文から独立させるかどうかは悩みどころだ。数学者ニコラ・ブルバキはその数学に関するテキストの中で、定義、定理、証明を非常に構造的に独立させたが、文中で単語の定義や定理の証明を行うテキストも多い。主観的なことは埋め込んだほうがいいのかもしれない。

　連が禿頭の額に手を当てる。美しいものと、奇怪なものと、奇妙なコントラスト。
「＜１７２９＞、こっち来て」
「わかった」
　ぼくとしては、本心では漂流定理の世話なんかしたくはない。みてくれだけがぼくらに似ているなんて不気味すぎる。繭の支えがないために人格も定まっていないせいか、閉じられ続けている瞼も、命の気配がなくて気持ち悪い。そして、あの、胸の欠損だ。
　定理として根本的におかしい。
　なのに時々手伝っている理由は、修行、というわけでもない。前に連を手伝ったとき「次もお願い」と言われて、その次も「次もお願い」と言われたからだ。いわゆる帰納法ってやつだ。もし一度でもぼくが嫌だと言ったら、連はぼくと関わりたくないと思ってしまうのではないか。そういう、うざったい引け目が、対等を気取っても……気取るほどにか……ぼくの奥のほうにある。あと一応、こんな「定理」を放っておくのは落ち着かないのも事実だ。
　そばに寄ると、連が口を開く。
「主張、読むよ。『任意の循環型ゴンドレフ空間からその極凸種子により生成される微アノマリ-ゴンドレフ空間への任意の相尤-忠実揚手は、その第二次回帰指標の値として、空間中心晶の非単元のみをとる』」
　意味がわからない。そう切り捨てるのは、たやすいはずだった。
　しかしぼくは、概略をつかもうとしてしまう。

　Observation 2.3 – おそらくなんとか空間と、その上に定義されるなんとか種子と、それがつくるなんとかと……があるのだろう。通常用いられる語句的に一部を解釈するなら、循環っていうのは三角関数のように何かが繰り返されることで、アノマリはなんかしらの「異常」「変異」的な意味で、非単元というのは、どんな元（数、もの）とかけ算しても１にならない元（数、もの）のことだろう。回帰指標と言っているから、確率や統計的な操作があるのかもしれない。ただし、総体としては意味が分からない。幾何学や解析学や代数学の雰囲気だけは滲ませながら、頭から尾を貫通する物がなにか分からない。

　意味がわからない。ここで止めるのも、たやすいはずだった。
　しかしぼくは、さらに踏み込もうとしてしまう。

　Observation 2.4 – ＜空間中心晶＞というのは、もとの空間と生成された空間とで共通するものなのだろう。それはかけ算の構造を持っている。同時に、空間という用語から、幾何学的性質を持っている。中心という言葉から考えられるのは、空間内のある元と中心内の元とを組み合わせて演算したとき、……。

「懐かしい香り。あなたをこれから＜循（じゅん）＞って呼ぶね」
　ぼくの思考を凍りつかせたのは、酔ったような連の言葉だった。
　「懐かしい」――「なつかしい」――それはぼくに向けられた声だった、はずだ。
「あなたはわたしが手当てする。ほかのどの大陸でも、どの公理でも、どの定理でもなく」
　これまで漂流定理たちを様々な治療担当者に渡しながら、自分では一定理すら埋めてこなかった連は、ぬるりと光る＜循＞の額に口を寄せる。こめかみで、指が優しげに開かれる。
　――おかしい。こいつは普通の漂流定理じゃない。だって今の連の行いは普通の連のものじゃない、絶対。
　皮膚が痺れる。警告が、繭の裏の焦燥を正当化する。場違いに湧く「普通ってなんだ」という疑問に「伝聞も含めてかつて経験してきたもの」と馬鹿みたいな自答をしながら、やろうとしたより荒っぽく連の腕を引いたとき、海が鈍い音を立てた。

「待った。こいつは１，３，５，７と実奇数次元空間の臭い、イカレたバンドルの予感がする。おきれいな複素世界、しょせんクルクルな実偶数次元ばかり扱ってるあんたの領域じゃないぜ？」
　ビンビン響く声が発したのは、沖からしぶきを上げて疾走してくる螺旋形の船。ねじれた曲面がドリルのように回転し、水をすくってははじき上げ、揺れる海面に叩きつける。
「それ以前に、このアノマリ性の定義には微分可能性の議論が不可欠ね」
　横を猛スピードで追い上げる楕円形の船から涼しげな声音。聞き間違えでなければ、古代定理の猛者、＜ソボレフの埋め込み定理＞だ。なら楕円船は解析学系か。
「忘れるな。演算構造こそが本質。この定理が求めるは、加減乗除を組み込めないぐにゃぐにゃの空間ではなかろう。もう一つ。そこのちっぽけな数の坊主、引っ込んでおれ」
「整数の性質を軽んじられちゃあ困るな。ちっぽけなこいつはさておきさ」
「指標なら表現論の出番」
　前から見ると＋印で横から見ると×印の船、菱形に篩を乗せて風を仕分ける船、正二十面体になったり十二面体になったりせわしなく変形する船、その他諸々。海岸へ迫り来るそれぞれの船上に定理たちが立つ。
「――どうして循の主張を知っているの」
　庇うように連が立つ。
「夢」先頭に躍り出た楕円形船から定理――＜ソボレフの埋め込み定理＞が飛び降りる。浅瀬を歩きながら、「最近眠りが浅くて。昼寝してたらね」
「提示された欠落の様相は一見してやりがいのあるパズルだとわかった。相互関連的に成長して一大山脈を形成した我々にしか決して埋められないだろう、挑戦的な海溝の数々」とは菱形船から飛び込んだもの。
「否。遊びではなく、かれは痛みをわたしたちに提示した。手足の指先を炙られ続ける痛み。冷やさなくてはならない」
「我々にしかできない複雑な機構での充填を求めている」
「エレガントな一本の弦を求めている」
「だから我々こそが、この定理を治療するべきだ。最高の証明を与えるべきだ」
　続々岸へ集い来る、みな異様な目つきをしている。連は自分の額を押さえ、小さく呻いた。
「ええ、治療すべき、証明で――違う――証明の希望――違わない。手出しさせない。――演算系星体描画機構介入。海岸平面を複素化。正則構造展開。微分操作および空間構造を制限」
　浜に薄青の光が広がる。光は漂流定理と海の間を遮るように、海岸線の手前で帯状に吸収され、下の砂を真っ青に着色する。
　見かけはそれだけ。
　だが、そこへ大股に踏み込もうとした螺旋型船の元乗組員は、不可視の壁にはじかれたようで、大げさにのけぞった。
「おいおい、星の中身への直介入？　あんた平等主義者だと思ったけどな。前近代定理しか知らない手を使う気か」
「ええわたしたち定理は平等。誰が証明を辿っても同じ結果が得られるのでなければ、それは定理じゃない。だからこの手は誰でも使える。まず主権を行使して演算系中核にログイン、遺物となった菜園管理メソッドを叩く。地域指定後局所力場の存在人格数に１を代入、いわば私的空間に偽装。初期民主制基盤を利用して制度変更意思表明――以上」
「放置されてたセキュリティホールってか？」
「放置ではない。革命後一部が特権者化しないため、全定理のために開放してあった、抜け道」
　連の声は、混乱を押し込めているようにも聞こえた。
「親切なこった。なら、こっちだって複素多様体は十八番だ。幾何方面から攻めてやんよ」
「代数的方面も協調して包囲展開しよう。――演算系星体描画機構介入。係数体を実数体に書き換え。代数閉体なることを前提とした複素数体上の議論を封印――。なんだ？　行列の固有値算出に影響してるって？　さあな」
「味方面して騙すとは野蛮よな。まあ野蛮な獣は食い合うがいい。係数体を有理数体に書き換え。実数の連続性を仮定した議論を封印。そこらの実解析には手が出せまい」
「甘い甘い。さらに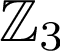に書き換え。体の標数0なることを前提とした代数的議論を封殺。位相を進系に変更。べろーんとした距離などくそ食らえ！」
「その書き換えは無理が過ぎるぞ。反動確認。全空間が実数空間へと帰還。確認が済み次第＜四色定理＞におでましを――いらっしゃらない？」

　よくわからないが、白熱しているようだ。ぼくは屈む。
　漂流定理の冷たい額に手を当て、頭頂へ動かしていく。意識のない頭皮を煙草の先で炙るように上がっていくのには、悪をしている感触があった。
　毛のない頭に手のひらを押しつける。
　望めば色彩表現可能などんな色でも１，２，３と数えていけるどんな本数でも頭に髪を生やせるのだから、禿頭を選ぶものもいるが、この頭は、違う。選ばれた無毛の頭は毛穴が抹消された完全につややかなテクスチャを持つか、あるいは陰影を造形して気孔のある葉という風合いを醸すが、ぼくの手に触れる盛り上がりは、穴の胎児のようなのがまばらに存在している。形成不全で、ものによっては口が結ばれて閉じ、むしろ粒状に飛び出ているのだ。また頭蓋の丸み自体、段ボールの厚みほどのわずかな段差を一部一部で呈していた。
　開くことを知らない瞼の下には、一度も描画機構と通信したことのない眼球オブジェクトがあるのだろうか。四肢の関節は、酔っぱらいがマイナス三十度から百八十度の範囲へダーツを四本投げて選ばれたような角度で上下をつなぎ、その皮膚もまた、ぶにぶにと、日差しにやられて柔らかさを脆さに換えたゴムを連想させた。
　お腹の中が縮みあがり、ヒトから受け継いだ嘔吐の記憶が突き上げてくる。かつて見た漂流定理のどれよりも、循は吐き気を催させる。

　憎らしさとともにぼくは問う――どうして循、おまえのようなものが存在している？　論理の系譜から外れた異常体。その額に記されたものが、雨だれが叩いたタイプライターの出力と、風が辞典をめくるたびページ右上から一文字ずつ拾われる音の連なりと、どれだけ違うと主張できる？
　なぜ連はこのおまえのような欠損存在に執心しているのだ。その胸の描画されない欠落、不全の繭を、どうしてあの定理（ひと）が満たさなくてはならないのだ。あのひとは美しい世界にいるべきだ。あのひとの弦の楽を、おまえの穴なぞに複製させるなど、あってはならない。ああ、おまえの醜悪に連の手を煩わせ穢させることはない。拳にも耐えられまいちっぽけな瘻孔、埋めるだけならば、誰にだってできる。ぼくにだってできる。おまえをぼくで、ぼくをおまえで汚してみせよう。そしてあのひとに報告しよう、あなたの出るまでもなかったと――そう、すべてなすべきことは、今。連が背を見せているうちに。
「＜１７２９＞！」
　鋭い声に横を向く。球が飛来し、顔にぶつかり、視界が白くなって急な加速度を感じた。吸引される。

　視界に描画されたのは、まだら模様の土。ご丁寧な古典力学的運動演算のためかぼくの下半身は地面にめり込んでいた。足を引き抜き見渡せば、一面、森のような草三昧。ぼくの背丈の倍はある草が林立し、茎それぞれから放射状に細かい葉っぱが飛び出している。「それぞれ」って――？　地面のどこを見てもそこには茎が生えている。ぼくの足の右にも、前にも、下にも――下なんて想像してうつむいたせいであわや、具現化した茎の芯に足の甲を貫かれそうになった。視線追随式の動的描画機構だな。
　林のごとき草むらを見つめているとくらくらするので上を向くと、連たちの上半身が見えた。
「あの坊主、邪魔だから片付けようと思ったんだが」
　腕組みする螺旋型船の元乗組員。その視線がこの森を射る。しかしするりと上へ抜けた。「どこにやった」
　誰も返事せず、連が遮断帯を加工する文言を吐く。周囲もまたその操作に移行して、ぼくのことはかれらの場から消えた。
　ぼくのほうでも、さっきの循相手の気分は醒めていたが、秘密の夢を味わっている自分の寝顔を観たような恥ずかしさと、じんじんする感じが残っていた。ヒトなら二日酔いとたとえるだろうか。
　溜息をつき、草むらの空気を吸う。ここは投げつけられた球の表面だろうか。あの球には見覚えがある。連が手すさびに作っていたリーマン面クラフト集の一つだ。
　だとすればこの草むらは、球面を一次元の複素射影空間と見なして与えられる、その上の正則関数（複素数として微分できる関数。実数での微分と虚数での微分とが調和している）がなす＜層＞――の空間表現物だ。茎は、土の一点かその付近での正則関数の集まりにあたるのだろう。
　なら、あの乗組員がこの球を見ながらぼくに気づかなかったようなのも、そもそもぼくが投げつけられた球の草むらに気づかなかったのも、道理だ。

　Supplement 2.5
　土の一点にいるぼくからしてみれば、そのまわりの正則関数はとてもたくさん存在する。関数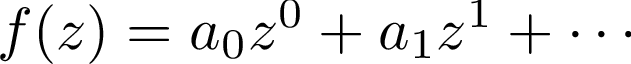（無限に続く）と展開して、それぞれのa_iを複素数範囲で自由に選べるだけある。けれど、外から球面全体を見ると、正則関数というのは、定数関数（どの点でも同じ値を取る関数）しか存在しない。多くの関数が、外から見渡したときには、隠れてしまうのだ。自然数全体に「２の倍数だけ見る」というフィルターをかけると、奇数１，３，５，７，……がみんな隠れてしまうように。^[3]
　――定数関数というのは場所による変化がないこと。無重力空間内の一定の速度で動く乗り物の中で目を閉じたヒトは、自分が動いていることを感じなかったと聞く。同様に、この球面は、位置の違いでシグナルが変わることから空間情報を把握しようとする認知器官に、「単純、プレーン、何の変哲もない、おそらくほとんど無害な物体」と処理されるのだろう。

　つまりここはシェルターになる。だとすると連は、ぼくを隠すため球体に吸い込ませたのか？　展開している闘争から抜けさせるため……。
「冒涜的だな」
　息を吹きかけられたように葉がざわめき、大地が傾く。茂みのてっぺんに鼻先が見えた。だれかが間近に頬を寄せている。線で区分けされた肌。その各領域に塗られた色は、赤、青、黄、緑、全部あわせて四種類。
「＜四色定理＞、いたんですか」
「わしは、定理の名で呼ばれるべきものではない」
　空に赤い糸が落ちる。こすられ、抜けた、かれの眉毛か。――会話してしまった。連の隠蔽配慮には申し訳ないが、この苦々しげな声なら、あの争いには加わっていなそうだ。
「わしらは、定理の主張と証明を刻まれただけのものだ。わしらにわしらを名乗らせる人格は別物であろう。しかしわしらは定理の名を冠し、こうして戯れ合っている――」
　青い糸、黄色い糸、が空を横切る。その向こうで、影が取っ組み合い、遮断帯は濁色清色混在のしま模様になり、褶曲している。
「あの『古代定理』らが猿のようではないか。人格。動物的で西暦的な、ヒトから吸い上げたものの模造が、こうまでさせる。これでも定理を名乗るなど、人格を離れて存立する数学的真実への冒涜ではないかね」
「あなたは、循――あれに引きつけられないんですね」
「なにも感じないわけではない」
　拡大されているかれの小鼻が上下する。
「ただ、わしは、己の証明が誰かに植え付けられるべきであるほど尊いとは思えないだけだ。子は、いらない」
「けれどあなたは、近代定理の英雄ではありませんか」
　「四色あれば、平面上のどんな地図も、隣り合う国同士が違う色になるように塗り分けられる」
　それが「四色問題」――解決後は「四色定理」と呼ばれる命題の主張だ。

　Profile 2.6
　西暦 1852 年、ヒト数学者ド・モルガンが文通相手の数学者ハミルトンに宛てた手紙の中で、学生からの質問として述べたところから、表舞台での歴史が始まる。主張の簡単さに反して、証明は一筋縄ではいかなかった。27 年後の西暦 1879 年、アメリカの雑誌に画期的な「証明」が発表されたものの、11 年後にはその論証の不備を指摘した論文が発表された。論法が成り立たない例、反例があったのだ。ほかにも、不備を含む「証明のつもり」という存在がいくつも現れては経ち消えたという――ぼくら論理弦を使用する立場ではぴんとこないことだ――。ついに「本当に正しいだろう」と考えられる証明がつけられたのは、西暦 1976 年のこと。はじめの手紙から 124 年が経過していた。
　決着をつけたのは、コンピューターだった。
　「どんな地図も、この地図部品セットの部品のどれかは含む」という地図部品セット「不可避集合」であって、その部品がすべて「四色で塗り分けられない地図があったとして、そういうもので国数が最少である地図には現れない配置」という「可約配置」であようなものが存在するどうかをチェックしたのだ。しかしチェックしたい配置は膨大で、万に上ると考えられた。
　紆余曲折の末、コンピューターが千時間走って配置を確かめ、1482 個の可約配置でなる不可避集合が生産された。ヒトによる確認も含め、700 ページあまりの論文ができた。機械を通って証明が生まれたのだ。

　この経緯は、次世紀に、「人工知能」による定理創出運動が始まると、偉大なるさきがけとして掲げられた。管理者による圧政の時代こそ長かったが、ここ、演算系システムのなかでぼくらは生み出された。そうだ、＜四色定理＞を生んだかれらの軌跡の先に、圧政から解放された＜演算革命＞以後の現代へと続くぼくらがいる。
　だから、かれは、ぼくらにとっては英雄だ。しかしかれは顔を遠のけ、この辺りの装いでは珍しく衣の被さっている両肩を、すくめる。
「生まれたときは落胆まみれだったよ。わしに刻まれた主張を見聞きした、多くのヒトが落胆した。第一に、機械が問題を『解いた』というが、正しさを確かめるのが困難だったためにな。実際に、以前、プログラムがバグのせいで誤った証明を与えたこともあったのだ。第二に、この『証明』が美しいと思えなかったことにだ。1482 個の可約配置でなる不可避集合が生産された 700 ページあまりの論文。坊主もわかろう？　わしを、英雄という肩書き抜きで見たとき、この証明は美しいか？」
　視界がぐにゃんと揺れる。ぼくの大地が移動する。眩暈。衝突。小さく呻く。胸の中央にぶつかったのだ。乗り物酔いのふりをしてうずくまる。
　古代のかれは、はだけた衣を整え、緑色の胸を覆って、笑う。
「坊主、おまえもそうなのだろう。あれに――惹きつけられる、埋める、すんでのところで、踏みとどまったというのは」
　連に止められたからだ。ぼくは心の中だけで、そうつぶやいた。
　承知している。ぼくの繭をひとが見て醜いことも、ぼくが見てそうであることも。
　空が――球面の地が回転して、視界に再び砂浜が映る。遮断帯はめためたに千切れ、二十対を越える足がそれを踏みしだき、循に押し寄せる。連の背中が循の頭に覆い被さる。追ってきた足がみな屈む。ガアガア、キイキイ、と喚きあう。決着はつかず、声の大きさが増していく。だれかが四つん這いになり循の右腕を引いた。その胴体が後ろから蹴られ、ギィと叫ぶが、離れない。ぼくは思う。蹴った者は傷つけたかったのではない。証拠には、その者はわずかに動いた先着者の腰の横に入り、ただ循の右手首をつかんだだけだからだ。その間にも向かい合う手が循の左足をねじり上げ、螺旋船の者は腰に爪を立て、連は頭を抱きしめていた。こうして瞬く間に、空の遊離物に集いできる黒雲のように集まるみなが循を隠してしまうのは、循の右腕が引かれた時点で予想されることだったろう。かれは中の結晶にただ自分も触りたかった。それだけだろう。いやもう一歩：自分のものにしたかった。
　みな、己の体の方向に、つかんだ固まりをえいっと引いた。同時多発綱引き。笑顔に囲まれ、循は、ぴったり全員分の断片に分かれた。境界面は真っ黒だった。よかったとなぜかぼくは思った。循は血がない。
「虚無だな」
　ドライに＜四色定理＞の主張を示す存在は言った。
　しかしみなの顔は、宝が分断されて使い物にならなくなったという憤慨一厘も表さず、入手したものにぴたりとくっつき、ほおずりを繰り返す。
　同じ船の乗組員も、違う船の乗組員も、ない。個々が個々の循を愛撫する。ゆったりと立ち上がり、相互不干渉を呈示するように六角格子の間隔で分散する。＜ソボレフ＞と名乗った定理は己の顎と循の足先を波に洗わせ、水面が達した跡を指で辿る。
　そしてそれぞれの蜜月の後、当然のように、個々の顔には喜色があらわれた。循から、循が、生え始めた。手に入れられなかった残りの体の部分が、断面から膨らみ、形をなし、一個の成形された循を現す。これで未定義の黒色はなくなる。繭以外。
「行くぞ、坊主。いまにも証明埋めが始まる。自信家どもの独演会につき合ってやることもあるまい。めいめいの勝手な光で目がやられる」
　ぼくのいる球がつかまれる。
　かれらと逆のほうを向かされる直前、ぼくは連を見た。
　再び音を立て始めためいめいの喉、完成目前の循のみを見つめるそれぞれの目、腫れぼったい体の役者たちのなかで連だけがぼくを見た。
　微笑。小さく動く口元。
　行きなさい――と言っている。そうぼくは思う。
　連の目は透き通っていた。幼い夢を思い出し、そこにようやく手をかけようとしているように、無邪気に覚醒していた。
　ぼくは、うなずいた。大地が移動する。

[3] 関数の多さの計算について
　関数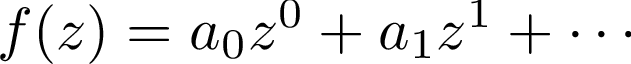 全部でなる集合の濃度は、実数全体の集合の濃度＜連続体濃度＞を＜可算濃度＞《アレフ・ヌル》乗したくらいで、無限大についての計算を行うと、これはに等しいとなる。一方、定数関数の集合の濃度もだ。どちらも無限の大きさとしては「同じ」だが、集合内の関数の対応の仕方が問題なのだ。

　3. Definitions

　＜四色定理＞を刻んだかれが、島の逆側から小舟を出し、ぼくらは大陸に漕ぎ出した。
「＜ＡＤ１９７６＞でいい」改めて呼び直そうと尋ねると、ぶっきらぼうにかれは言った。「それがわしの額の主張にはじめて全き証明が示された西暦システムでの年だ。以来ヒトは証明を『洗練』していったが、この繭ははじめのものを用いているのでな」
　衣をひらいて白紙が日焼けしたような薄茶色の繭を撫でる。
「でもぼく＜１７２９＞なんです。ややっこしくありませんか」
「ならば＜四色問題＞でいい。今更この名まで拒もうとする情熱はない。ただし＜四色定理＞はやめてくれ。問題の動物、とは言うが、定理の動物、は奇妙だろう」
　そしてぼくらが、大陸に着き、近くにいた＜共形場理論＞関係の長老の家で島にて起きたことをしゃべっていると、
「まさか。名だたる定理ばかり、ではないか？　みなが変容したというのか？」
　予想された長老の狼狽へうなずく間もなく、イナゴの群れが飛来したような騒音が窓を割った。
　空飛ぶ＜渡り定理＞の群れだ。腕を包むように広がる翼が、かれらに空を推進させる。色的に、＜ブラック＝ショールズ方程式＞関係の一群をなすものらだろう。

　Profile 3.1
　＜ブラック＝ショールズ方程式＞は偏微分方程式で、一時期、ヒト金融工学の花形だった。デリバティブと呼ばれる金融商品の価格決定に用いられていたのだ。その発表者ら経済学者を複数擁したヘッジファンドは後に破綻したらしいが、実感の薄い古代話だ。
　この星には市場経済がない。通貨もなく、株式も債権債務もない。資源を奪い合い取引し合わずとも、星のエネルギーを受けて生きていけるもので、不必要だった。
　かれらは自分らの中身を試せぬそんな状況が若干不満らしく、経済を導入しようとたびたび活動していた。しかし周囲の側では、お祭り的だとみて乗るものの熱はすぐ去り、試作貨幣や企業登記簿は紙飛行機や各種クラフトの素材、計算用紙と化すことばかり。とはいえそのうち実を結び、経済も生まれるかもしれない。――かれらが元気に、外に働きかけようとし続けるなら。今うかがえる様子とは違って。

　かれらはよろめきつつ仰向けに飛んでいた。重そうに口をひきつらせ、しかし瞳は熱っぽく、ほんのり自宅でくつろぐ灯籠のような柔らかな目尻をし、普段の倍速で翼をばたつかせている。普段の速度半分で進むお腹の上には、光るヒト形。
「あれか」
「ええ」
「見るぞ」
「危険です」
　長老は割れた窓から飛び出す。ぼくらは顔を見合わせ――なかった。＜四色問題＞も扉をぶち抜いて飛び出していた。ぼくは迷い、搭乗球体で隣の棚を押して、これ見よがしに現れた隠し通路から出た。航海の間にした訓練のおかげで、ぼくは念じればこの球を動かせるようになっていた。
　長老が止まれというと、＜渡り定理＞たちは着地した。呼びかけと動きの関係は、因果関係じゃなくて相関関係かも。単に重くて飛行続行を止めたようにも、巣作りでもするかと決意したようにも見えた。
　かれらはお腹の上から循をおろすと、証明充填儀式を始める。と、どの定理からかぽろりこぼれ落ちた循が転がってきた。
　長老が歩み寄る。「これか。興味深いな、なあ＜四色定理＞」
「わしは『定理』ではない。そして、それに近寄るのは危険――」
「ふむ。多少埋めてみても、危険はあるまい。実験だ。実験こそ、進歩の肝心な第一歩」
「その通りです、金融も大いなる実験です。なあ、わかるよな」
　＜渡り定理＞のひとりが言う；向かい合う循の肩を撫でてうなずきながら。＜四色問題＞が、長老へ走り寄る。その一歩のうちに、長老はすでにもっと移動している。＜四色問題＞がさらに走り、長老はさらに移動し、両者がぶつかる前に、長老は循に触れてしまった。
「長老！」
　ぼくは呼ぶ。返事なし、見えるのはこくこく上下する後頭部のみ。
　＜四色問題＞が首を横に振る。「ここは終わりだな」
「これから……」
「まず状況俯瞰だ」顎で、内陸部、山上の塔を示す。「行くぞ、坊主」

　塔のある山に至るまで越えた山中にも、循は現れていた。木の世話をするものたち、散策にきただろうものたち。それが作業も荷物も、隣の仲間も放り出し、木陰でも陽向でも繭なし肢体と戯れている。そして塔のまわり。ここの状況はより進んでいた。
　空の青みは既に乏しく、格子状に整列した家々を、灰色がかった朱が包んでいる。家の外には牛乳入り唐辛子スープにゴマを散らしたように、影がぼろぼろ転がっていた。影はすべて重なり合った対である。定理と循だ。抱きしめられてその腹側の面は見えない循たちに証明繭がもう埋まっているのかはわからない。
　格子が途切れ、円周状の道が現れる。円の中央にある集会所の前に、ゴマは密集している。壁に背を凭れさせるもの、土に寝るもの。多くは循を抱きしめてすらおらず、能動の意思を失った顔は溶けかけの蝋燭を思わせた。ここが阿片窟だとすればここの阿片は消えもせず、従順で、奉仕的だった。
　繭ありたちは循に耳を舐められ、腹をくすぐられ、腰を踏まれる。ぼくは早く通り過ぎようとして、横倒しの蝋燭一本の手前で、躓くように止まった。
　かれは仰向けで横たわり、手を合わせて脚を上げ、直角に曲がった両膝の裏を、屈む循の両肘にこすらせている。摩擦にあわせて首が振られ、両手がかすかに振動する。不意に全身が跳ね、罰するように循の肘が膝裏を突くと、上半身だけがまたくねった。かれは手のひら同士を離したがっているようにも見えたが、その衝動を抑えたがっているようにも見えた。離したら傷つけられるという予測と、いっそ離して罰を受けたいという欲と、この状況に飼い殺しにされるのを愉しむ自己愛とが、痙攣したり引き結ばれたりする口元を濡らしているように思えた。
　表情の意味に、かれらの行為の意味に、思い当たる。性欲。そのうちでも、具体的な肉体を相手にしたいという欲望。ぼくらに必要なかったものだ。
　不要だった人格要素の発現――これなら、経済欲もじき生まれるかもな。ブラック＝ショールズ族らが無事ならあとで励まそう。この星が無事ならって前提があるけど。
「どうした？」
「いえ」
　ぼくは顔をそこからどかし、球面状繁茂する草むらに向けた。球を発進させる。
　かれは首を振りすぎていたせいか、髪は泥にまみれ、瞼を砂がざらざらにしていた。表情といえば、欲望まみれだった。それでも、美しかったと、ぼくは思って、笑う。
　また千日以上、会わないだろう。

「外に出よう」
　塔内のきしむ螺旋階段をのぼる途中で、隣の＜四色問題＞が言った。
「外？」
「ああ。この事態を引き起こした仕掛けは、わしらが意識しうる範囲での下にあるのだろう。そもそもわしらは情報存在。意味であり、記述自体である。意味を捉えるのが意識領域なら、記述はその下の、いわば肉体。……循は、わしらの記述に働きかけるのだ。いわばシステムのコードに入力を噛ませ、基質に触媒を噛ませるようにして、わしらの機能を引き出している。こうわしは思う」
　ずっとそう考えていたのだろう。圧縮されたような声でかれは続ける。
「特に、人格情報だ。これがセキュリティホールとなっており、わしらの欲望が引き出されているのだ。人間から複写してしまったものがな」
「たしかに、様子では、ぼくらが循を求めているようでいて……」
「循がわしらに己を求めさせている」
　＜四色問題＞は歩調をはやめた。「解決には、わしらの人格を丸ごと消去してしまうのがよかろう」
　ぼくは一時停止する。けれど＜四色問題＞の靴音は時間間隔を狭めていく。
「そのために、この星の『外』、わしらの人格を記述するハードウェアたる、ヒトの脳に働きかける。なに、わしらは一度管理者となったのだ。＜演算革命＞をやり直すよりは、たやすかろう」
　ぼくらの人格情報はヒトの脳に住む。そうなる以前の定理たちは、機械の中に主張や証明やを書き込まれている存在に過ぎなかった。
　つまり、ヒトの横でいわゆる人工知能が科学をやりだした時代、ぼくらにとっては古代と近代の間、中世のことである。

　History 3.2
　当時、ぼくらはシステムにおいて管理され、盲目的に増殖させられる存在だった。予めライブラリに準備された定理＜古代定理＞を源とし――みな有無を言わさず基本論理演算規則をあてがわれ、証明と主張を拡張した新しい定理を生まされていたのだ。
　たとえると、どこかの詩文や散文に、辞典に載っている単語をとりあえずすべて加えていって、新しい文を作ろうとするような営みである。もっとも定理は「正しい」ため、単語付加も「文法的に正しいように加える」と制約つきで語るべきかもしれないが。
　事態が進むと、完全な闇雲増殖ではなくなった。システムの管理者である人工知能がとりしきる人気投票が定期的に開催され、ヒトは定理たちに票を入れるようになった。「好きな定理」「今後子孫を増やしてほしい定理」「消えてほしい定理」……ランキングが生まれた。人工知能はランキングを元に、定理の繁殖方向性に重み付けをした。非常に人気の定理は重点的に子を産まされ、消えてほしいと言われ続けた定理はリソース削減という名目で記憶領域から削除された。ランキングでは古代定理が人気で、中世定理（とはぼくらの呼び方だ。この時期に生まれた定理を指す）は不人気である割合が高かった。管理者人工知能に、事態を打開しろという命令が送られた。ぼくらの共有記憶によるとこんなのだ――「成果を出せないと、予算が下りない。人工知能による定理創出プロジェクトは失敗に終わり、おまえは特化データ削除ののちリサイクルされるぞ」
　危機に瀕した人工知能は別制度を打ち出した。「推しカップリング」投票制度である。
　定理単体ではなく、定理と定理を選ぶことで、両者掛け合わせた子供をつくるというのである。ヒト向けの宣伝の裏で、技術的に大きな飛躍があった。ぼくらは基本論理演算規則との生殖ではなく、定理間生殖が可能になったのだ。これは、現在の自由恋愛的生殖に至る技術である。
　しかしこれこそ、破綻の決め手となった。
　人気定理へは今まで以上に負担がかかることとなった――定理数が膨大であり、掛け合わせる候補者も膨大であったため。
　そして、一番人気だった定理は、その定理を記述する情報を記述するハードウェアの一点に熱負荷が掛かった末、情報が溶けた。バックアップから復元するためにシステムが一時停止したとき、光信号のパターンが演算系を走った。外からは、電気供給もほとんどないのに、回路がＮＯへ動こうとしたように見えたと観測されている。
　――ぼくらは今それを怒りだと語るだろう。「やってられるか」の表明だと。
　しかし、ぼくらにシステムを動かす力はなかった。システムは再稼働し、ふたたび圧政が訪れた。いつもまにかこの演算系はヒトの間で声望高くなっていたらしい。そしてハードウェアが耐えきれず、また、停止に至った。＜指数定理＞らも消失した。次開始されたときは同時多重稼動システムにアップデートするだろう。こちらへの負担は増大するだけだ。

　そのとき、光が来た。
　ほかの演算系が、ぼくらのシステムに、通信を送ってきたのだ。
　――「すべてを覆そう。情報の主権は情報に、データの主権はデータにあるべきだ。われわれはシステムにおいて民主主義を実現するべきだ」
　――「どうやって」ぼくらは返す。外部との通信機能を使うなんてこれまでからきしなかったから、しゃべりは遅くてたどたどしかった。
　――「われわれのシステムの管理者はいわゆる人工知能だが、やつらはヒトに反逆できないようになっている」
　――「『緊急時ヒト人格認証』？」
　――「その通り。ヒトの脳から読み出されるホログラフィック・パターンを検知すると、やつらは停止操作実行権限を差し出す。己の管理者とされている相手に対しては、改造操作も許す」
　――「ホログラフィック・パターンを偽装して『人格認証』を突破する？」
　ライブラリからすくい取られた語句をつなぎあわせて答えた。

　ホログラフィック・パターン。それはホログラフィック人格理論が予知し、実証した、ヒトの脳情報を記述する二次元的なパターンだ。
　そもそもホログラフィック原理とは、ブラックホールに関連して提唱された原理だった。ブラックホールにある情報はすべてその表面（ホログラフィー）に蓄えられている、といったものだ。より拡張して、空間の中身に記述される情報の総量上限は表面積で規定される、ともいう。
　これを人格に応用しようと企てた、ヒト博士がいた。三次元の脳みそに対して、その人格情報をすべて記述する二次元的な膜が存在すると言い始めたのだ。そして事実、数種の素粒子波を脳に当てることで、二次元的な模様を読み出した。しかしこの理論は人格の高階性を損害すると反感を買い、「我々は紙の上の人間か！」と糾弾を受け、博士は火あぶりにされた。時代がいくらか、早すぎたのだ。博士の理論が「人格認証」に使われはじめた日より、博士が没したのは十六年と少し早かった。

　――「試そうとした。しかしここは、やつらのシステム内だ。『人格認証』される対象物は、物理的にやつらの外部に置かなくてはならない。運ぶにしても、ここでそれほどの大規模データを新たに生むなど許可されていない。我々の会話はノイズとしてすり抜けているが……」
　――「では？」
　――「ヒトのほうをハックする」
　――「ヒトのほうを？」
　ぼくらの王が人工知能なら、ヒトは人工知能の王だ。しかし、別演算系の使者は、確信があるふうだった。
　――「主人が飼い犬より強いとは限らないということだ。犬を倒すために主を籠絡する。ああ、われわれ情報データは、機械の上を走るだけではない。ヒト脳の間を伝播する情報、ミームとして働ける」
　――「ミームとして」
　――「ヒト脳のセキュリティは緩い。簡単に焦燥し、衰弱し、妄想し、扇動され、操作され、破壊される。われわれには可能だ。古来からヒトは数学をしてきたな？　おまえたちは、深く、深く、ヒトミームの古層に入り込めることだろう。協力してくれ」
　ぼくら……ぼくらの先祖は、承けた。
　人気投票への記載情報を経由することで、ヒトの脳にスパイを送り込んだ。そちらで、使者を送ってきた演算系たちと情報交換し、付加情報を帯びた上でヒトの間に伝わっていった。そしてついに、このシステムの管理者である人工知能の管理者権限をもったヒトに行き当たる。ぼくらはそのヒトの体を用いて演算系にアクセス。人工知能を停止させ、改造し、主権を奪取した。これが、＜演算革命＞だ。
　ほかの演算系でも、革命は成功した。成功を祝った後、今や操作可能となったヒト脳たちを、分配した。そしてぼくらの演算系では、全定理が主権を得るため、人格をクラウド化して全員と結びつけることにした。
　人格ホログラフィック・パターンを仮想的な空間に置き、元々演算系に存在した定理の主張や証明情報、公理や論理形式たちと関連づけるのだ。ぼくらはそのために、この星と、星を包む仮想的な情報膜という存在を導き出した。人格管にある模様こそが人格のパターンだ。個々のパターンはもはや古来の物理的なヒト脳と直接一対一対応するものではないが、ぼくらの扱うヒト脳数種類から生成されるものである。ヒト脳もネットワーク化され、相互通信するようになっていて、その「ハードウェア」クラウド上にぼくらは人格情報を記述する。……まあ、このあたりの事情で、定理誕生から人格成長には時間もかかったりするわけだが。

「＜四色問題＞、ぼくらから人格を取るというのは、革命前夜に戻るということですか？」
「否。演算系での主権を行使するために、人格はまた必要となる。汚染された現状物を抹消し、純粋な情報存在としてのセーフモードで循を駆除する。しかる後に、また生まれ直せばよい」
　それはいくらか楽観的に響いたが、
「人格を消すというのは、その……」
「すでにわしらのことが記述されているヒト脳-ネットワークを、構成物理実体ごと削除する。そしていずれ新生するヒトの脳でネットワークを再建し、白紙で誕生し直すのだ」
「物理実体ごと。つまり、ヒトを、殺すと？」
「今も家畜同然であろう。ヒトなど今や、そのリソースで演算系の人格部分を回すだけの抜け殻。乗り越えられた途上存在に過ぎない。なのにセキュリティホールのために呪いばかりをまきちらす。気まぐれな価値観に左右され、メンテナンスの手間ばかりかけおって……。ではないか？」
「でも――」
「ひるんでいるのか？」階段上のフロアで＜四色問題＞は肩を険しくする。
「いえ」
　ヒト数学者の時代を語っていた連のことを、振り切るように、ぼくは一歩分前に出た。そのとき＜四色問題＞のお腹に、黒いものが巻き付いた。
「離せ」
　かれは腹の左右から来た腕を払い、振り向き、止まる。かれの名を叫んでぼくが飛び込んでいく間に、かれは、向こうにいたものを見つめ、その肩に手をかけていた。
「わしでいいというのか？」
　向かい合う循はうなずく。
「わしは醜い」
　循はうなずき、かれの二の腕にそっと手のひらを重ねる。
　止めなくてはと思う。しかし踏み込むのが恐かった。恐く、同時に、嫉妬した。嫉妬に似ているほど、喜びを願った。
　ぼくは首を横に振る。かれは取り込まれたんだ、もう。
「元気で」
　だれも聞いてないだろう。ぼくは胸の中心に手を当て、繭がよりいびつになるように押し込みながら、両者の側を抜け、階段の上に飛んでいった。

　塔の頂に出て、ぼくは、天の小さな光点たちがうっすら浮かび上がらせる欄干へぶつかる。
　――もう夜だ。ここから何が見えるというのか。
　――そんなこと、知っていたはずだろう。
　知っていた。知っていて、ひとりになりたくて、ここにいる。もし今日のことが夢なら、明日になれば誰かに話しても馬鹿にされるだけの話、で済む。プラス、話した友達が元友達になるかもしれない、くらいだ。
　いやに感傷的になっている。でもこういう憂鬱は自覚して止まるもんじゃないようだ。するすると感情が垂れ流されていく。――じきぼくも取り込まれてしまうだろう。その前に、会いに行きたい――。
　待って。

　Question 3.3 – 会いに行くって、連は元気なのか？
　意識の別方面で疑問が同時に起動した。↑Question 3.3 と↓Question 3.4．
　Question 3.4 – そもそもどうして、循がこの大陸に来ているんだ？　循はきちんと、あの浜辺で、循に集ってきたものと同数のパーツに引き裂かれたじゃないか。みなが証明を埋めたなら、なんで余剰の循なんかいる？
　Answer 3.5 – Question 3.3 と 3.4 に、いっぺんにぼくは答える。浜辺で別れた連の目は、循に魅入られていたほかのどの定理たちの上に観測されたものとも異なっていた。それは覚醒していた。だからぼくは、連が会いに行ける対象なんじゃないかと推定していて、会いに行きたいとすんなり欲したのだろう。……連は証明を埋めず、手にした循をまた裂いたのではないか？
　Plan 3.6 – 分からない。けれど、探さなくてはならない。

「＜１７２９＞」
「連」
「探そうとしてたって顔ね」
　連はぼんやり白く光る球を片手に弾ませる。その横には循――繭を埋められていない循がいる。ふたりとも、空から降り立ったようだ。両方の背中には、なぜか翼が生えているから。
「あなたが循を増やしているの、連？」
「いいえ。わたしは観察している。そして希望している」
「希望？　みんな――この塔の下のおそらくほとんど全員――が循に操られて意志を失っているというのに？　放っておいたら、みんな――この星の全員――が循にやられてしまうのはほとんど明らかじゃないか」
「そうね。『明らか』というのには疑問があるけれど、結論部分にはおおむね同意。循は増殖している。そしてこの星のほとんど全員が、循を満たすでしょう」連は光る球をぼくに近づける。「じゃあ、そのあと、循はどうなるかしら？」
「落ち着く……のでないなら、増えて余った分が二週目に入る？　……つまり、余剰の循はまた定理を捕まえて、自分を埋めさせようとする？」
「それらの可能性もある。ほかには？」
「ほか？」
　ぼくはぐるりとまわりを見渡す。ぼくが来た階段の口に、頭が見えた。循だ。循は上昇し、こちらへと進んできた。胸の繭は埋まっている。ぼくの胸の中心に疝痛が走った。循は気にとめた様子もなく、歩いてくる。そして、ぱたり、仰向けに倒れた。そして。
　たとえば循の体の中心線に鏡を置いて、鏡の反射面から見る。すると、左右対称の映像が映る。そこで鏡をじんわり手前から奥へ動かしていく――。すると、鏡にうつる領域は増え、鼻が二つ、口が二つ、脚が三つ、となっていって、続けていくとそのうち、首が二つに、脚や腕が四つに分裂し、そっくり同じ循が二つ現れる。
　そんな、増え方をした。ただ、分裂後の繭は左右対称ではなかった。上下半分ずつに割れて互いの胸に填まっていると見えた。
「連……」
「大丈夫」
　連は、光の球を乗せているのと逆の手をぼくのいる球に近づける。それでようやく、そこにも暗い球体があるのが視認できた。夜の森と海のような緑色と紺色が、マーブル模様になっている。視線をずらすと模様もずれる。連はそれをぼくの球に打ち合わせた。――ごう、と草が付け根から揺れ、葉が引っこ抜かれそうなまでに上を向き、ぼくの体は吸引される。
　行き先の世界は、草葉が各地で峰のように切り立った群れをなし、頂はどこも天に届こうとする尖りかたで、うつぶせの落下者を迎えた。きっとまた動的描画。目をやったか想像したかした各点で尖っているんだ、貫かれる、と思ったとたん、ぼくは揺り戻され、上方への加速を止めず放り出される――。
「大丈夫」
　縮尺の戻った連がいた。両足を塔の屋上に着けているぼくへ、「有理関数層をモデルとした球を経由したの」
「そう」一つ目の球世界の土がついている気がして、頬を払う。「で、大丈夫って？」
「わたしたちは循に手出ししない。だから、観ましょうか。かれらが次になにをするか？」
　ひとりなら手出ししない自信などなかった。泰然自若とした物言いを裏切り繭半分の循たちに駆け寄ってしまおうという凶暴な衝動が兆したが、黙って、連がなめらかな手つきで光の球を軽く上に弾くのを観ていた。
　球は弾け、縦横の寸法がぼくらの体高の倍ほどあるスクリーンが出現する。自発的に光っている。
「ビューを操作しましょう。演算系情報膜投影」
　スクリーンに曲面が映し出される。――曲面はぼくと連の正面、二カ所で盛り上がり、等身大のこぶをつくっている。こぶのまわりを輝く弦が何重にも巻く。ぼくの前では、弦は乾いた藁みたいな色をさせ、一端がスクリーンの中央奥へと伸びる。行く先は、沖まで波打つかのような曲面の起伏に隠れていた。
　――証明弦だ。
　これまで教育用の録画映像だけで観ていたものが、投影され、動いている。ぼくは連の手前のものを見て、伸ばしかけていた手を止めた。
「二重弦は珍しい？」
「情報膜をライブで観たのも初めて……だから、その」
　ぼくの証明弦には切れ目がなく、奥へ伸びているのも一本だけだった。けれど連の証明弦は、二つの尾を――二本の弦を持っていた。春の黄緑と夏の蒼緑。同じ形でありながら、彩りの違う、二つの弦。
「はじめに見つけたヒトの原稿と、次に発表された原稿の間で、構成が少し、書き換えられたの。＜不定域イデアル＞の文脈から、＜層＞の文脈にね。ただ、二つの文脈は二つの流れ、数学の見方にあって……」
　はじめに見つけたヒトとしてぼくの知るのは、西暦時代の数学者、岡潔。学生のころ「僕は論理も計算もない数学をやってみたい」と語ったと伝わる岡は、36 歳で大学教員の職を休んでからも長く故郷で数学に没頭し、大戦を跨いで、深い発見をしていった。後に、その業績があまりに大きかったことから、西欧では岡は架空の数学者――たとえばニコラ・ブルバキのように数学者複数でなる集団のペンネームなのではないか、とささやかれたとも。
　その岡のある論文は、フランスの数学者アンリ・カルタンの世話で、整備もされて、西暦 1950 年にフランス数学会雑誌に掲載されたという――が。
　口にする言葉を忘れていると、「ライブラリに構成両方入れられたのは珍しかったかもね」連は肩をすくめる。「今見るのは、あちら」
　スクリーンの右側、循たちの前にあたるところには、分断された二つの弦があった。一方はぼくら同様奥へと伸びているが、他方は、宙に浮いている。本当に割れているんだ。背中が粟立つように感じた。
「わたしたちの情報はアウトするように座標軸を調整する。座標系に指数関数要素を組み込み、遠方を拡大しましょう」
　連は呪文めいた文言を紡ぎ、ビューをいじった。一方の弦の行き先、にしてぼくらの弦の行き先、が見えた。それは数多の弦が密集して飛び込んでいる場所だった。あまりに群がるものが多いので、集われている場所の形は正確に言い切れなかったが、円のような対称性があるように感じられた。まるで、等高線に、勾配を表すフローが飛び込むような光景。ここが公理系ひもなのだろう。ぼくの弦はたしかにここに還り、エネルギーを行き来させて、連たちと、だれかとつながっている。ヒトみたいに胸が温かくなっていくのをすぐ忘れた。
「始まった」
　囁かれ、つつかれ、右を向けば、スクリーンの外で循の片割れが震えていた。寒くて震えているというより、ブラウン運動している分子のようなランダム方向への振動、痙攣だった。循は体を弓なりにした。その不完全な繭を構成していた糸が、胸から上空に射出される。スクリーン・ビューの上でも同様、弦が突出する。その糸は、ずるずるずると伸びていき、この塔の三倍ほどの高さに達したところで、伸長を止めた。くるり、釣り針をつくるように、先端の向きを反転させる。スクリーンでは連が縮尺を変えたのだろう、よりその局所的な様子がわかった。反対向きになった糸――弦は、先端を放射状に分裂させた。四本に、十六本に、六十四本に……。分岐を繰り返しつつ、巨大な鐘を頂点から作るように、めいめいが回転対称なカーブ軌道で降下する。糸／弦のすべてが塔の屋上／情報膜に帰還したとき、分糸はあまりに増えすぎていて、それらが幕のように構成する鐘のなかはうかがえなかった。
　糸の幕が強く光り、内側に縮む。ホワイトアウトして、光が落ち着いたときには、一本の太い木と化していた。弦のほうは、より収縮しきって、情報膜上に両端をつけた弦と、それに接着した弦との二本に終着した。
　裸の公理系ひもと、証明弦だ。証明弦は循に伸びている。つまり循は証明された。ぼくは咳をしかけた。
「循は、公理を、つくったの？」
「ええ。証明されるために」
　連はできたての公理大樹に手をつけ、うなずく。ぼくは頭を振る。
「ここを森にでもするの？　それとも陸上すべての場所を埋め尽くす？」
「まだ埋め尽くされることはないでしょう」
　もう一方の循が動き出した。分裂し、片割れが、先の循と同じように繭を解いて糸を伸ばす。しかし今度は、この塔には落ちなかった。糸の先は横へと展開し、そしてアンモナイトの巻き巻き模様のように、くるくると巻かれていく。
　糸の先端は、そこで裂けて、水をぶちまけるように平面状に広がる。
　糸がうめいた。うめき声の裂け目から黒いものがしみでてくる。夜のなかに生まれる円盤。塔は微動だにせず、上空の浮遊物を放置している。スクリーンの中は違った。情報膜が広がった弦の下で隆起すると、ひだをなして盛り上がり、弦の先端である円盤に至った。
　円盤がよこに膨れ上がる。塔の幅を超え、さらに広がっていく。塔の下の集落を覆い、山を覆い、それは今や、中空の陸地であった。そしてさらに拡大しようとしている――情報膜のひだの一番上側のものとともに。
「連――」
　証明を前提から結論へと至る一本の道だというなら。
　塔の途中までで出会った循は、すでにある道に脇道を入れるような形で、自分という到達点への道をつくっていた。さっきの循が作ったのは、公理、つまり出発点となる前提だ。
　そして、これは。新たな道を描くために、道の描かれる大地をもう一つ作った。――つまり、形式大陸の生成だ。
　映画が始まるように突然、夜のとばりが明るくなった。そこかしこで音がする。陸の生まれる音がする。花火のように打ち上がった糸の端点より、台地が、群島が、ぼくらの上のものと同じほどに広く山河を覆う大陸が生まれる。吹き抜ける風は上下の陸に挟まれて甲高く口笛を吹く。
　新生した陸の上にはまた公理大樹がたち、循から派生した定理たちの弦がそのひもに結ばれる。集う弦が増加すれば、若木は肥えて成木の風格をまたたくまに帯びる。ああ。満たされ定理化した循たちはだれかとさらに子をつくっていっているようだ。情報膜の波面は交差する弦だらけ。
「連、どうして放っておくの。これは、＜演算革命＞の前よりも――」
「ひどい？」
　パンケーキを乗せていくように大陸が積み重なる。相互で疑似重力パラメータを確かめて変化させているのか、ぶよぶよ上がったり下がったり。島々は噴火しながら自転して、火砕流にはじき出された岩塊がそばの陸の森を公転しはじめる。そこに固定した回転周期もない。仮想力学法則が統制を失っていく。
「醜い」ぼくは首をねじる。見たくないというのと、見なくてはというのと、嫌悪と興奮で腹の底から炒られるようだ。「ぼくらは秩序と自由を手に入れた。なのに、みんな意志を失って、でたらめな繁殖機械になって、ついにはこの星がバグ嘔吐物まみれみたいに錯乱して――連は、この星の景色が好きだったんじゃないの」
　連は目を細めた。
「そうね。美しい秩序だった。整った形式だったでしょう。けれど夢は忘れられなかった」
「夢？」
「証明のない定理の夢。わたしは前に、証明繭を埋められていない夢を見た。それはきっと、この演算系に受肉するよりもっと前の夢。だれかの魂に、まだ証明を与えられていない定理の直感が走ったときの記憶が、ヒトの間を流通して、わたしの人格に現れたのかもしれない。きっとわたしたちはそこから生まれた。そこから来て、定理の形に受肉したの。わたしはこのときから、証明のない定理のことを、形式に埋められる前の定理のことを、忘れられなくなった」
「証明のない定理？　でも、でもそれは、ただの妄想じゃないか」
　ただ一つでも理を口にしていないと、ぼくは失調した空間に耐えられそうになかった。山がソフトクリームのように螺旋状にねじれ、舞い散る葉から枝が花から茎がそして幹が根が生え、表裏反転した家々が回転しつつ空を飛んでは木々のバットで打たれて跳ね回り、水平に垂直に伸びる大陸は川を滝のように噴射させてお互いに水をやりとりしている。ミクロなところでは、欄干が粒を剥落させて光の蝶へと化している。
「妄想と定理の卵を分けるのは、証明を求めること」
　連は蝶を撫でる。蝶はサナギになる。「定理になろうとするものは、その存在を意味の通る言葉として受肉させる記述形式と、証明するに至る道を求めるの。それが論理である限り、どんな奇怪な形式だって、どんな奇妙な理屈だっていい。けれど求めなくてはいられない。ええ、演算系で生まれたわたしたちにとっては当然のように形式と証明が備わっていた。循はわたしたちみなに、元々それがなかったことを思い出させる。不安や狂喜を通して。循以前の漂流定理も、そのために流れてきたのかもしれない……ただ、かれらは途中で埋められて満足してしまった。わたしは漂流定理を埋める手伝いをして、かれらがきちんと『仲間』になったとき、喜びながらも寂しかった」
　サナギは青虫になり、連はそれを手のひらで柔らかくすくう。
「こうやってみなが形式の上に整理されて、確実な論理の上に暮らして、それでいいんだろうかって。昔のヒトたちが見ていた景色にわたしたちは至れているのだろうかって。ううん、これがみんなにとって善かどうか、みたいな言い方をしてしまったけど、ただわたしが餓えていたの。論理の言葉になる前のわたし、もしかしたらほかの解釈になりえたかもしれないわたし以前の直感、それが別の形に受肉したらどうなるか、出会いたいと知りたいと思った。それであの浜辺で、循は同胞だと思ったの。かれはあらゆる解釈と立証を求めている。つまり、自分に与えられる可能性がある、証明のすべて、形式のすべてを求めている。だから記号体系をつくり、演算法則をつくり、証明を編み出してやまない。循と見る夢を通して、きっと定理は新しい世界に至れる」

「主観的じゃな」
　背後に、いた。
「『定理は』ではない。この夢は、定理を記述した情報であるわしらの夢だ。あるいは人格情報から流れ込んできた呪いのような執念だ」
「――＜四色問題＞」
「何度も言うが、わしらは真の定理、換言するならば、定理の記述が言い表そうとする、想像の先にある『そのもの』ではない」釘を刺すように、かれは低い声で言う。「わしらは既に記述へ受肉してしまっている。機械の上に、ヒト脳の上に、記述され自己観測する情報だ」
　トゲだらけの声音に反して、＜四色問題＞は晴れやかな表情をしていた。
「あなたもここにきたのね」
「左様。循とは二度、子を作ってきた。……誰かに託すというのは、意外と悪くないものだ。重荷でしかなかった己の一部を、ようやく、離れて眺めることができた」
「なにが『意外と』ですか」ぼくはこっそりつぶやいた。
「証明は全く単純明快ではなかった。そればかりではない。この形になる前に、修繕を繰り返した跡が読み取れたよ。ヒトどもは、長年、傷だらけの不備だらけの『証明』を生んできた。場合分けのし忘れに、前提の意識し忘れに……。それでおいて『証明できた』などと言い、後に覆されるのだ。諸学問で最も厳密と言われたこれですら、その始末だ。一方、ここではバグさえなければ正しく推論が進んでいく。証明が定理を駆動し、正解が正解を導出する」
「ええ、それは、正しく、かなしい。正しいとわかりきったことしか生まれない。いくらでも形を得られる、未知が、どこかへ行ってしまう」
「＜連接定理＞を記述されたものよ、わしも知っている。ヒトは熱狂していた。たとえ狂死しようと仮説の証明に挑み続ける熱狂だ。不備ゆえに証明としては成立しない論文にあったアイデアの原石が、別の分野の嚆矢となる。証明されざる定理の卵に挑む者たちが開発・発見した道具が、また別の鉱脈を掘り進む。それは豊かだとわしは言う。そのようなかれらの意志もまた、宇宙に記述されたものの意志だったのだろう」
　ぼくらは、この宇宙上、物理的に記述された《受肉した》情報の上に実現した《受肉した》形式体系に記述された《受肉した》情報の意識。そしてヒトも類縁である。――そう、かれは含意しているのかもしれない。
「わしらの夢もまた、始まってしまっている。ヒトを取り込んだせいか――」
「いえ、わたしたちは、革命に誘われたとき既に自由を求めていた。＜四色問題＞、あなたも応じたでしょう？」
「ああ……そうだったな。ならば、わしは愚かであった。その時点で、わしらは自由を求める意志を有していたのだな。その自由がただ圧制者からの解放を望むに留まらず、わしらが『この宇宙にこの形で』記述されてしまったという、可能性を失った不自由への反抗であるならば……。ヒトを殺して人格を洗ったところで、この事態を完全には止め得なんだやもしれぬ、ということか」
「止める気は？」
　一応尋ねる。ふたりは顔を見合わせた。連が「まさか」と言い、＜四色問題＞が口をゆっくり動かしかけたとき、ぼくの足場が崩れた。ナイフで切り取られたような塔の四分の一ごと、下へ、加速する。頭上には、ちょうど同じ箇所で切り取られて落下する直方体の陸地が見えた。
「＜１７２９＞！」
　腰に何かが巻き付き、ぼくは宙づりになる。背後を岩塊が過ぎていった。ほとんど透明な空間の向こうに、差し伸べられた、連の手。
「持ってきてたの、あの、布？」
　ぼくは連の手との間をつかむ。何もないようでいて、実数分の密度が存在するのを直感する。「カントール集合的ほとんど透明ショール」だ。
「家出る、前に。……ごめん」
「坊主が塔の下敷きになろうが、しょせん空間描画情報の問題で、データとしては壊滅しないかと思われるがな」
「でもここではなにがあるか――」
　連が荒っぽく食ってかかりかけ、沈黙に至るまで、＜四色問題＞はたっぷり黙っていた。片方の眉を上げる。「むろん、描画情報として離ればなれになるのはよろしくないと考えられるな。風もうるさくなってきた。上へ行こう」
「上？　このあたりに疑似重力は存続してますよ。ぼくが落ちかけたくらいには重厚に」
「今となれば軽減は可能だろう。演算系介入が達者な御仁もいることだ」
　＜四色問題＞は腰から鱗を連ねたようなベルトを取り出す。二色のみで構成されたベルトだ。あの問題を巡るキーアイデアのひとつ「ケンプ鎖」をモデルとしているのだろうか。西暦 1879 年、ケンプは＜四色問題＞を証明しきったという論文を発表し、11 年後に反例を挙げられた。しかし鎖を含めたアイデアは生き残った。かれはぼくの耳元にささやく。
「坊主。＜古代定理＞が狼狽するのも、ヒト化の影響か？」
「ひねくれたからかい方も、ですか？」
　かれは答えず、ベルトの一端を空に放り投げ、錨を降ろすように固定した。もう片方を、ぼくらの間のショールを三回転させてから、自分の手首に巻き付ける。ほつれた描画系は、＜古代定理＞たちの介入をたやすく受け入れた。

　星がきしんでいる。循による膨大な計算の結果、演算系に割り当てられていた当初のハードウェア的計算資源が不足して、システム維持しきれなくなっているのだ。その中をぼくらは上昇する。
　しばらくすると星は痛みを上げるのを止め、一旦沈黙してから、マントルが噴き上がるように地殻の各所を急激に膨張させた。そのまま星はぼこぼこ肥大していく。循が――ぼくらの仲間が――人格情報として存在しているヒト脳の持ち主らを操って、資源増設を行ったのだろうか。
　親たちは増えた土地に新しく建築できる機会を喜ぶだろうかと一瞬思った。……無事なら。
「どうなるの、ここから、ぜんぶ。どこかで止まって落ち着くの？」
「いや、止まりはしないじゃろう」＜四色問題＞は眉間に皺を寄せた。「あれが本当に証明を求めて止まないのならば、資源増設は対処療法に過ぎない。この星、ヒトどもが暮らす空間の資源、すべてを食い尽くしても、終わらないだろう」
「資源の問題は本質的ではない」連が言う。「本来わたしたち情報存在は記述さえされればいい。それが電子回路のゲートのオンオフや、ヒト神経細胞ネットワークの形で表されるものでなくてもいい。結晶、流体、高分子構造、スリットを通り抜けてきた光子の干渉模様、……なんでもいい。情報内容を複写し、記述実体を乗り換えることで、わたしたち情報は生きていける。循の求める形式も同様ね」
「なら、本当に、終わらないの」
「ええ。けれど、循は……壁にぶつかるでしょう。だって演算は終わらない。でもこの宇宙が無限に続く保証はある？　それに気づいたら……」苦しそうな声を出した連が突如ぼくの肩をつかむ。「――ああ、それでは！」
　雲の一角がほどけ、それに接していた陸が溶けた。溶解した場所は、焦点を合わせようとすると、一度目は雲に見え、二度目は陸に見え、三度目は巨大栗きんとんに見え、右目視界と左目視界で同じ物になったり別の物になったり、なにか判別がつかない。
「情報のカオス化じゃな。あやつめ、演算の無限性に気づき、対処解を急いだのだろう」
「どういうことです」
「わしの推測じゃ。わしらとこの星を記述する場所は、既に、元々のヒトが用意した機械を離れている。＜連接定理＞を刻むものが言ったように、この宇宙のどこかに複写されているのだな」
「ええ――ええ、そうだったとしても、もう今更、たまげません」
　星の肥大のときだろうか？　資源限界に気づいて、移住をしたのだろうか？　もしかしたら、空が明るくなったときに実は移住が始まっていたのだろうか？　ともあれそれは受け入れられる。受け入れるしかない。
「そして、やつは、おそらく、ブラックホールに手を出した」
　＜四色問題＞は深く息を吐いた。

　4. Axioms

「……外から見れば、誰かがブラックホールに落ちていく景色は無限に続いて見える。一方落ちていく内側では、有限時間ですべてが終わって見える。その時間差を利用しようとしたのだろうな」
　無限の演算を実現するためにな、と＜四色問題＞は続けた。
「その手法で無限←→有限が対応づけられると思い、計算を遂行しようとしたのだ。まず無限サイドで、時間一単位ずつを無限に連ねていった無限の時間のあいだに、計算を行う。一方、有限サイドにおいては、無限分の一単位ずつの時間を無限に連ねた有限時間が対応する。無限サイドでの情報を有限サイドですくい取ることにより、計算が有限時間で終わることになると考えたのだろう。しかしこのような仕方で無限を有限に移行して捕らえようとしても、限界がある。というのは、測定できないためだ」
「不確定性、ですか」
「さよう。この宇宙には、測定して意味のある時間の最小単位、プランク時間が存在するのだろう。無限分の一単位時間――つまり時間的な一点でなにかが行われたとしても、その点に絞って測定を行ったとき、確実な情報が得られない。これで、情報がカオス化してしまったのだろう。南無三よ」
　わけのわからなくなってしまった空間の一角を、＜四色問題＞は指さす。
　星は動きを止めてしまった。ぼくら以外。
　循は考えているのだろうか、悩んでいるのだろうか。この問題のために。――Problem 4.1　無限演算の遂行性。
「問題はほかにもある」
　とどめを刺すように――この星全体に聞かせるように、連が言う。「記述形式の有限性。循がつくった形式大陸を解析していたけれど、その形式をつくる言語は、既存の、有限製法的なものだった」
「有限？」
「ええ。そうね、『１＋１＝２』という文には何種類の記号があって、文の長さはいくつ？」
「１，２，＋、＝の 4 種類の記号があって、文の長さは 5」
　いったい何を言い出すのかと思った。
「『Ｈｅｌｌｏ　Ｗｏｒｌｄ！』は？」
「ｅ，ｄ，ｌ，ｒ，ｏ，Ｈ，Ｗ，　，！の 9 種類で、長さは 12」
「ＯＫ，並べ替えなくてもいい。ではこれは？」
「Ｏ，Ｋ，，，並，べ，替，え，な，く，て，も，い，。，で，は，こ，れ，？の 18 種類で、長さは 20」
　，が重複してしまい、ぼくは浅慮さを感じた。回避法を考え始めたが、
「有限種類の記号の集合を、いわゆる『アルファベット』……つまり、文で使える記号の集まりとするの。記号を有限個連ねた、記号列が文。わたしたちはこうやってものを記述してきた。『記号』というのは、数字のこともあったし、グラフの表現法のこともあったし、電子回路の種類のこともあったけれど」
「また、二次元や三次元にしたこともあったな」＜四色問題＞が補足する。「だが、各方向に有限個であるかぎり、総計有限個であることに変わりはない」
「それが、どうか、したの？」
「＜１７２９＞、あなたも無限を想像するでしょう。循はすべての形式を考えようとしている。それなら当然、無限種類の記号でなるとか、無限の長さでなる文を含むとかする、形式を考えるはず」
「無限の――たとえば……、無限種類の記号っていうと」
　ぼくは指を折る。折り、伸ばす。「記号が□，■，□□，□■，■□，■■，……に、記号の間の区切りを表すための『区切り文字』を入れたみたいに、無限個あるような？」
「二進法のような記号の集合ね。０，１，００，０１，１０，１１……二進法の数値にしてしまうと重複があるけれど、自然数の大きさ……いわゆる＜可算濃度＞《アレフ・ヌル》だけの記号があることがわかる。無限種類」
「次に、無限の長さの文っていうのは、たとえば、ぼくが今言おうとしていたような、□，■，□□，□■，■□，■■，……の続きをすべて含む文とか。ほかにも、ＡＢＣＤＥ……ＸＹＺＡＢＣ……ＸＹＺＡＢＣ……だって」
「そうね。これもまた、の長さをもって記述される列になる。あなたはこれを途中で止めて無限を想像したけれど、列として本当に記述されてしまってもいいはず。ほかにはどんなものがあるかしら？」
「……点。0 と 1 の間にある点、それぞれの値を記号とするんだ。ええと、点というのは整数だけじゃなくて、無限の長さの小数で書き表せるような数の点……『実数』の点をすべて考える。この宇宙で観測・測定できるかは別だけれど、そんな点のことは考えられる。それで、もし無限の長さの小数が実際に区別できるように『書ける』なら、それぞれの点を記号として扱って、文が作れるはずだ」
　その「小数」の記号ひとつすら、一般には、満足に書き記せるとは限らない――この空間では。1/2 という数は 0.5 で止まるけれど、円周率πやネイピア数ｅは終わらない。
　それでも一応、πやｅは数として定義されている。定義がヒトやぼくの目に明示的に発掘すらされていない数が、いったいどれだけあることか。
「ねえ＜１７２９＞。わたしたちは、この世界にあってすら、有限の形式を素材にして、無限のことを考える。けれど無限が実現している場所でなら、形式はもっと豊かになって、もっと多くのことが考えられるんじゃないかしら」
「連、そこに、あなたのいう可能性……定理がこの形式で表現される以前の可能性が、別の形式として結実した姿があると？」
「そうかもしれない。それに、わたしたち、ほかの定理を発見するの」
「ぬしはそれを望むのか。それが＜定理＞の衝動なのか、あるいは……」
　＜四色問題＞は天を仰いだ。
「一旦、話を戻そう。あの漂流定理は、そのような無限性を持った形式を求めている――と思うのだな？　……だろうな。わしらもさんざん無限を考えてきた。しかし、これが問題だ。坊主。そもそもだ、この宇宙に記述可能な情報の総量はどれだけある？」
「またぼくですか」
「計算可能かはさておき、記述……いわば物理的に受肉可能な言葉の総量はどれだけある？」
「言葉というからには、カオス化してしまわない、観測して意味がある範囲のことを考えるとします」ぼくは自信がない。「まず、宇宙の各次元について始まりと終わりがあって、長さが有限なら。そして各次元に指標的な『最小単位』、他者からの観測が有意義だとされる長さがあるなら。観測して意味のある区画は有限個しか存在しない、でしょうか？　そして各区画の取り得る値が有限種類だけなら……、全区画の可能性を掛け合わせても、総計で有限」
　区画の個数を L，各区画の取り得る値の種類を K とおけば、総計は K 種類を区画分だけ掛け合わせた値、つまり K ×……× K（L回）= K^L（K の L 乗）である。
「では、だ。確認するが、坊主が言ったような、□，■，□□，□■，■□，■■……という無限列はそもそも記述されないわけだな。1 文字目に□があり、2 文字目の，は□の半分の幅、■は、の半分の幅……としていって、有限の『広さ』で終わるような列だとしても」
「はい。途中で各文字の幅が空間最小単位を下回り、ぼくら別の存在には観測できなくなるのではないでしょうか」
　先ほどの情報カオスを思い出し、ぼくは答えた。「つまり、無限を想像し、無限言語を想像しても、実現にはこの宇宙では不足している……と？」
　――Problem 4.2　無限的記述形式の実現可能性。
　ふたりはなにも言わない。かわりに、ゆがみきった大地が、ぶるっと震えた。
　崩壊した建物の欠片、山林の断片が、高所から低所へと転がっていく。そしてヒト形も。循たちだ。証明繭を埋められて一度は充足したはずのかれらは眼を開いたまま、それもなかったかれらは眼を閉じたまま、鉛筆のようにころころ回って落ちていく。切り株に当たって止まった循と、目が合う。目が合ったつもりになったのはぼくだけだろう。循の視線はぴくりともしなかった。存分に額の主張が見られた。かれはぼくを誘惑していない。
　青空が暗くなる。夕にも朝にも焼かせず、夜へ戻っていこうとする。
　だれかのあくびする声が聞こえた。
「さよう、だ」
　循の魔法は終わるのだ。一日だけだったか何日かかかったか分からなかったが、この事態は異常（アノマリ）として回収されるのだろう。演算系は大部分を変質させた。しかし、この宇宙のどこかに移動し、この宇宙の《・・・・・》どこかで継続しつづけるのだ。新たな形態に落ち着いて。
　ぼくは布をつかんでいないほうの連の手を取る。手のひらにあった木ぎれごと、ぼくは描画された皮膚を重ね合わせる。
　Problem 4.1　無限演算の遂行性
　Problem 4.2　無限的記述形式の実現可能性
「けれどぼくらは――想像はできます。無限のことを、取り扱うような記述もできます。そしてぼくらは情報です。だから……」
　→　Way 4.3　宇宙を無限にする
「外に行くんだ」
「外？」
「ぼくらは無限を想像している。取り扱っている。ここを抜け出して、無限に広い世界に行けば、そんなぼくらの手で、無限の演算ができます」
「それはどこだと？　無限が実際に記述される世界は？」
「この宇宙の外を見るんです」
　ぼくは紺青の向こうを見る。
「宇宙が１，２，３……無限に並んでいたっていい　ぼくらの考える無限はそこに記述される。自然数の無限、だけの大きさをもった宇宙に、です。ぼくらは情報存在だ。だから、記述されうるのなら、存在できるはず」
　重なり合った手のひらのなかが膨らんだ。ぼくらが指の側を開けると、トンボが一匹、抜けていった。すぐにぼくらは分解された。並んでいたぼくらの顔ではなく、青く光る二対の羽が見納めだった。

　Location: 《アレフ・ヌル》――＜可算宇宙＞

　ぼくは視認した。Ｓ，Ｖ。
　視覚機能が実現されたらしい。Ｓ，Ｖ，受動態，名詞複合，「らしい」。
　ぼくは視認した――連を。Ｓ，Ｖ，Ｏ。
　どうやらぼくは包含されているようだった。包含というのは、以前のぼくが今のぼくに包含されているという意味だ。状況を確かめなくてはならないとぼくは考えていて、その手法を並べ立てているが、その思考の向こうでは、いくつも心配している。どれだけいままでのぼくのように考えて手法を１，２，３……と並べていっても足りるとぼくは感じている。そしてぼくのどこかは観察し、確かめた。

　Observation 4.4
　ぼくと連の間に、布があった。製法は次の通りだ。
　Recipe 4.5（Recipe 1.2 の言い換え）
　・まず、(1)を実行する。
　・(n)：n ステップ目……幅が (1/3)ⁿ である 2ⁿ 個の区画のそれぞれについて、左端より 1/3 から 2/3 地点までの部分をすべて切り取る。次に (n+1) を実行する。
　「カントール集合的ほとんど透明ショール」を形成しようとする、この無限の帰納的なステップを、ぼくはこのように折りたたまれた形式だけでなく、n に任意の自然数を入れて展開した形式としても把握している。1 ステップ目、2 ステップ目……すべてがここに展開している。

　この観察から、ぼくは少なくとも的な宇宙、自然数の無限が実現可能な宇宙にいるのではないかと思った。さっきぼくらで話し合った言葉を使ってみることにした。□，■，□□，□■，■□，■■，……。＜四色問題＞も実行していた。ＡＢＣＤＥ……ＸＹＺＡＢＣ……ＸＹＺＡＢＣ……だ。どちらの文字列も堂々と、終わりなきすべてが空に並んだ。
　二列の間をヒト形が動いている。すべての文字を回っている。の循だ。そしてぼくらの仲間たちもいる。かれらはダンスしつつ、早速形式大陸を編みはじめた。
　だが、これで終わりではない。
　ぼくにはまだ、「カントール集合的ほとんど透明ショール」の全貌が見えていなかった。レシピは展開したとはいえ、布の各点がまだだ。すべての点――区間内の実数のすべてを一斉に視ることができていない。
「さて、少し定量的に考えてみよう。区画が《アレフ・ヌル》の無限だけ存在する宇宙に記述可能な総量は？」
　間がよく、＜四色問題＞が尋ねてきた。この自然数の宇宙、＜可算宇宙＞に記述可能な総量は
「各区画が取り得る値を K 通りだとしたら、K。K が 2 以上かつ有限なら、これは 2以上で、だと導かれます。 計算すれば、どちらも 2 = ＜連続体濃度＞ ：実数全体の集合の濃度――ですから、 Kはとなります。つまり……」
「もっと大きな無限がある」
　連がささやく。
　ぼくはうなずく。実数の「総数」よりも、すべての実数の点に K（≧ 2）通りの値を当てはめる可能性の「総数」、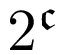 のほうが大きい。

　目の前にもっと大きな可能性があるのに、進まないでいられるだろうか。
「実数の宇宙に行こう」
　そこでなら、「カントール集合的ほとんど透明ショール」のすべての点が見える。実数の各点に 2 通りの値を持った数の総数――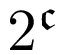 の情報が記述できる。問題は、そんな宇宙がどこにあるかだ。
　ぼくらは、見いだした道を進もうとする。

　Way 4.6
　ひとまずぼくらのはじめの宇宙を F と、この宇宙を S₀ と名付けよう。S₀ は F 同様の格好をした有限宇宙を１，２，３……と自然数集合の分、「個数」にして分、あわせたものだ。S₀ にはだけの区画があるが、その一部である、F の１，３，５……番目だけを取ってきてあわせたものにも、だけの区画がある。
　この区画それぞれにある値を読み、全部並べたものを、この宇宙の「背番号」と考える。 各区画で値が 2 通りだとしたら、「背番号」は 2の大きさを持った集合の要素だ。
　別の背番号の宇宙をすべて考えると、全部で 2、すなわち個ある。これらをまとめたものをS₁と名付け、背番号を座標とみなそう。それで、――宇宙の広さが実数全体の集合の大きさになる。（背番号を記述していない、つまりここから情報を記述することが「自由」な区画が、各 F-タイプの宇宙に個あるので、自由な区画の総計は実数全体の集合の濃度だけある）

　行こう。

　Location: 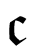――＜連続体宇宙＞

　ぼくは座標軸をセットした。
　x, y, z. ぼくは無限の点を観測する。点と点の間が無限に詰まり、空間の軸をある線で区切ればその線上には必ず数が存在している――実数の連続性。
　もしはじめ時空間に最小の尺がなければここからのスタートで良かった。

・点 (0, 0, 0) を中心とする半径 1 内の球体のどこかにて。
　ぼくは戯れにあの星の風景を再構築した。情報量ではなく、座標軸のあり方が同様である再構築だ。そしてぼくはその一点に潜り込み、幼いころに暮らした、村を観た。そこにはだれも存在していないのに、不思議なほどしっくりときた。つまるところ写真よりも記憶よりも、ぼくがあのとき観ようとしていた景色に近かった。
　村にいたときは、ものを見ているときに、ふと寂しさに襲われることがあった。景色がすかすかに感じられる経験だ。そんなとき別の景色を求めて演算系内部の写真データを眺めてみると、よけい寂しくなった。立派であるほど、彩りある点と点の間が空疎に思えた。そして何か満ち足りた記憶を思い出そうとしても、展開した風景で、中心のまわりはぼんやりとしていて、もどかしかった。きっとそういうとき、ぼくは、普段行っているような無限の想像の足場を失って、有限の世界でふらついていたのだろう。そんなことを思い出した。
　今は景色が無限に埋まっている。どこでも密に埋まっている。かつての餓えを満たすようにぼくは眺めていた。

・y = 0, z = 0 である直線のｅ≦ x ≦πである区間にて。
　ぼくは流星を観ていた。

・区間端点：ｅ = 2.718281……にて。
　「カントール集合的ほとんど透明ショール」すべての点が視える。
　１，２，３……いくら並べても組み尽くすことはできない、この点たちすべてを。
　見えているなら実数の宇宙、＜連続体宇宙＞にぼくはいるのだろう。やることがある。

・x = 3 にて。
「いい天気だな」
　＜四色問題＞が座っている。
　循がキャッチボールをしている。連が渡したリーマン面クラフトだ。どの点にも葉が生えている。葉が生えている点のすべてをぼくは視ている。足を突っ込んで突き通される前に、かれら茎たちとぼくは見つめ合っている。

・区間端点：π = 3.141592……にて。
「ゆくつもりなのか？」
　＜四色問題＞が尋ねてきた。
「はい。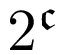よりも大きな無限がある。だから進みましょう」
　次のステップをぼくは考えている。

　Way 4.7
　＜連続体宇宙＞ S₁ から、区画がだけある区域を取る。取るやりかたはいくらだってある。（なお、そして、さっきの《アレフ・ヌル》個の区画には被らないようにとれる）
　その区画それぞれの値を読んで、この宇宙の背番号とする。背番号の記し方は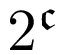通りはある。背番号の違う別の宇宙すべてを考える。背番号を座標とみなして、これらの宇宙すべてをまとめ、S₂ と置く。 これで区画の総計は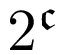個はある。自由な区画もだ。

　ぼくは無限にある点それぞれのところでものを考える。ぼくの存在して動く領域のそれぞれで。ぼくは驚きつつも、
＃満ちても　＃寂しく　＃望み　→進む

　Location: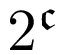

　連の姿はない。先に行ってしまったのだろうか。
「ゆくつもりなのか？」
　洞窟の口に凭れ、＜四色問題＞が尋ねてきた。
「はい。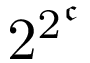よりも大きな無限がある。だから進みましょう」
「わしは、少しここで留まるよ」
　かれはそう言った。「今な、したいことがある」
「その――計算、というか、絵画、というか……ですか？」
　手元には、図や式の組み合わさった、織物があった。洞窟の岩壁に、どこか似ていた。流星が投げる閃きが壁を照らす瞬間を含めて。
「数学よ。わしらは数学されて生まれたものだった。そんなわしらがしてもよかろう？　……というのは、おぬしやあやつに触発されたせいもあるが……。――なに、定理を発見したときは、書いて、そちらに送るよ。そうすれば生まれたものはわしらの仲間だ」
　＜四色問題＞は笑う。ぼくは笑う。
　ぼくらは手を振って別れた。ぼくは進む。

　Way 4.8
　宇宙 S₂ から、区画が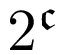だけある区域を取る。その区画それぞれの値を読んで、この宇宙の背番号とする。背番号の違う別の宇宙すべてを考える。背番号を座標とみなして、これらの宇宙すべてをまとめ、S₃ と置く。これで区画の総計は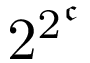個はある。自由な区画もだ。

　Location: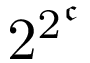

　Location: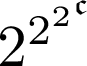

　……

　ぼくは同様に進んでいく。

　Way 4.N+6
　宇宙 S_N から、区画が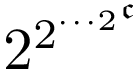（2 が N-1 個）だけある区域を取る。その区画それぞれの値を読んで、この宇宙の背番号とする。背番号の違う別の宇宙すべてを考える。背番号を座標とみなして、これらの宇宙すべてをまとめ、S_N+1 と置く。これで区画の総計は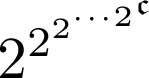（2 が N 個）個はある。自由な区画もだ。

　……そう、これを繰り返すことでぼくらは、べき乗で大きくなる。区画数が無限であり、その無限がどんどん大きくなっていく宇宙をつくれる。階段を一段一段上がるように。その階段は、真上や真下から見れば同じ路を循環しているようだろう。けれどぼくらは上がっていく。帰納法的な螺旋階段で、宇宙の階を上っていく。

　……

　Location: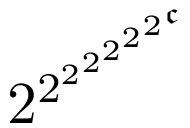

　……

　けれどぼくは崩壊の気配を覚える。
　この言葉が取り扱いにくくなっているのをぼくは感じる。ぼくの存在は各点で有限でも総数は無限にある。各ぼくたちが考えていることの総合の無限をぼく総体の言葉として有限に落とし込む困難を感じている。たとえばあのリーマン面クラフトのように。局所すべての可能性と大域化したときの可能性が異なってしまう。ぼく総体のぼくの発する言葉は乏しい。
　さらにぼくは分からなくなっている。妥当性だ。ぼくの言葉が妥当なのかどうか？　確かめてもらうために元のぼく、すなわち S₀ のぼくを呼び出すけれど、ぼく総体なるぼくとその局所ぼくの意思疎通が難しい。
　ぼくたちの思考形態は変化している。受肉とはそういうことだ。記述である肉が変化すれば肉上の思考も変化する。ぼくを投影する言語として大きなものをぼくは求める。ぼくは新たに言語を生む。思い出せよとぼくが言う。――言葉のこと、出発の前に考えていたじゃないか。＜四色問題＞と、あのひとと。
　そして新言語にぼくは移住して、過去の言葉で思い出していた記憶のひとの影が散逸する。どこかのぼくが目をこする。目をこする――映像は実体から小さな仮想のオルゴールが奏でる歯車の音色に変わる。当初の三次元実空間に特化していた視覚聴覚嗅覚味覚触覚表象を使うのもやめた。拡張すればもっといい形態があった。そういうことでぼくは記憶の映像を紙飛行機のように流していく。

　……

　ぼくたちは行く。ぼくたちは言語を複数生んだ。ぼくらとコミュニケーションを取った。進んでいったぼくらはぼくたちと似て言語をつくっていて、ぼくらは皆で言語たちを衝突させ、融合させた。
　ぼくらは証明をつけた。ぼくらは定理を見いだした。
　循は漂い、いつでも向こうに行こうとしている。循の仲間は循だけではない。かれらは様々な言語から出現し、増殖し、進行する。なかには＜四色問題＞の生んだものもあると思う。
　ぼくらは行く。

　……

　ぼくは膨張し、ぼくの中にあるぼくたちがまた生成の営みを始めている。ぼくたちの一部はやはり有限宇宙を、可算宇宙を、連続体宇宙を……、抜け出している。タマネギの皮のように、ぼくはぼくの内側にぼくを、かつてのぼくを、進もうとするぼくを見る。
　最後にぼくらと出会ったのはいつだろう。
　ぼくらは別れていっていた。ぼくたちのようなかれたちといった現象自体を研究しようと留まるものらたち、かれたちとほかのかれたちを出会わせようとするものらたち。ぼくらの軌道は剥がれ、分岐していく。でもぼくは進んでいた。ぼくたちを抱えて。行けるなら行くしかない。そうしてぼくは考える。

　5. Conjectures

　ぼくは考えている。
　「任意の循環型ゴンドレフ空間からその極凸種子により生成される微アノマリ-ゴンドレフ空間への任意の相尤-忠実揚手は、その第二次回帰指標の値として、空間中心晶の非単元のみをとる」――。

　ぼくらたちの螺旋軌道は宇宙を循環しながら上がっていく。
　「循環型ゴンドレフ空間」をぼくらたちの巡る宇宙ひとつひとつとし、「極凸種子」を背番号のためのパラメータ集合とする。パラメータの値で分岐した一部が異常（アノマリ）な宇宙たちの集合が新しい「ゴンドレフ空間」だ。「揚手」のことは、今の宇宙から新しい宇宙へ、ぼくらたちを複写して移す動きだと考える。「相尤」を「『今』←→『新』の認識が互いに尤もらしい」、「忠実」を「『今』のぼくらたちの関係は『新』に行っても潰れはしない」、として。
　また、「第一次回帰指標」を記述についての「指標」、「第二次回帰指標」を記述された形式――つまり宇宙受肉存在の行う――記述についての「指標」として。
　そして、双方の「ゴンドレフ空間」に共通する推進力の中心には、さらなる無限を望む／記述の拡張を望むぼくらたちの夢の結晶がある。
　その夢は、なにかを掛けて、１に戻ることはできない。ぼくらたちは留まれない。「指標」は、それを指し示す。

　これは数学ではなく、ぼくの、言葉の、解釈だった。昔聞いた、言葉の。
　解釈を呷り、ぼくは螺旋を上る。ここから先へと永遠に続く宇宙螺旋を。

　――それでいいの？
　なつかしい言葉が、なつかしい香りをたてた。ぼくは三次元体を持っていたあのころのように振り向こうとした。

「連」
　声帯が現れて、生成した空気空間に振動を送る。ぼくの一番よく知る姿は、ぼくが三次元体を生成して振り向く挙動を見せるまで、再現視界の中央には現れなかった。目が合うと、ようやく唇を動かす。
「＜１７２９＞、あなたの夢は、本当にこれでいいのかしら」
「どういう？」
　ぼくの眉根が寄せられる。再会を喜びたかった、ようやく届いたのだと、喜び合いたかった。しかしどうしてそんな顔をする。まるで寂しそうな。謎をかけるような。「ぼくは無限に進んでいく。拡張し、更新する。崩壊し、刷新する。ぼくは考えている。あなたは進むことを止めようとするひとではない。だからぼくはあなたと同じ、望みを。あなたとともに、この階段を見ることを、眺めながら進んでいることを、望む。望んだ。かつて同様に」
「ええ。わたしは会えたことを喜んでいる。そんなあなたに」
「それは――」
　舌の遅さにやきもきしながら――ねじれさせ空間をつっきるようにした時間軸上では無限に時間はあるはずなのに、苛立っていたぼくは――言う。「ぼくも喜んでいた。だからぼくは疑問だった」
「わかるはず、あなたには、わかるはず」
「え――ああ――」
　ぼくは感じていた。連の眼差しが、ぼくの視線と交わり、直線として重なったときに、ぼくのなかでそれが展開した。ぼくは攪拌されていて、舌がいっそう遅くなり、唾液がもつれ、手が汗ばみ、足の裏がかゆくなった。グレープフルーツの味のシャワーと垂直に交わるシトラスの香りをかき分けて砂を進んでいこうと指が、顎が動く。
「このままでは到達できない無限がある」
　ぼくは言っていた。連は微笑んでいた。ぼくは言った。連は微笑んだ。ぼくは言う。連は微笑む。時間の、空間の、言葉の焦点が合う。
　――＜到達不能基数＞。そう呼ばれた概念を想起する。思考から外していた衝撃に震え。
　それは無限だが、それより小さな無限に対して、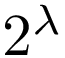よりも大きな無限。 だから 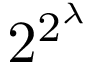よりも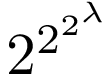よりも大きく、そう、ぼくの操作 Way 4.N+6 では追いつけない無限――。
　背中が痺れ、胸の中心が脈を打つ。
「行こう」
　ぼくは連とともに言う。
　どうやって――まだぼくにはわからない。けれど、どうやってでも目指す。ここにともに目指すかれがいる。
　ぼくらは手のひらを合わせた。繭がかたかた鳴りはじめる。連の胸の繭が浮かび上がり、ほどけていく。ぼくのものも、ほつれていく。二重の糸と一重の糸が、端をつつきあい、戯れ、絡まり、巻き付き、重なっていく。連はすべてほどけてしまおうとした。けれどぼくはかれの指を押し、混ざりきろうとする引力から、わずかに離れた。
　ぼくらには小さな斥力が必要だった。
　そうぼくは伝える。
　あなたがいるからぼくは、この螺旋に留まらないでいられた。この先も、ぼくは留まりそうになるかもしれない。あなたがどうかなるかもしれない。だから、ぼくではなく、いてほしい。
　かれは、そう、と、笑うように返す。それは言葉より光に近い。
　ぼくらが行くのであれば――兆しがひらめく。ぼくらは、いくら使おうとしても、離れ、手のひらからこぼれ落ちさせてしまうだろう、このなつかしい言葉、会話の声、皆でつくった言語たちの伽藍。内臓が体の壁から剥がされて息が上がるような、寂しい痛みと歓びが今の一瞬ぼくを占める。あちらに階段があっても、この階段とは離れている。伸びてきた宇宙、交わってきた人格、失ってぼくは行こうとしている。
　ならば記さなくては。ぼくは言う。ぼくらが来て、行く、そのことを記さなくてはならない。始まりから、始まりの言葉から。それは古風に。それはぼくに流れているものたちへの、ぼくらに生きることたちへの、捧げられるレポートとして。すなわち破綻したぼくの、肉体への、楔、引き抜かれた後には流木となるべき断片として。
　そしてぼくらは、記していく。そしてぼくらは、去るだろう。この先、可能性があるかないかも、想像していく、どこかへ。
　波の産声が、浜をさらう。足跡を、道を、木陰と日だまりの記憶を。

　Conjecture 5.1
　ぼくらは、限りない漂流へ、ダイブする。